A single ant can carry 10 to 50 times its own body weight and run 700 times its body length per minute. These are impressive qualities; however, when acting in a group, that single ant can accomplish much more.
In groups, ants build colonies, retrieve food, and even use peer pressure to influence others. They achieve this with pheromones - essentially, perfumes that ants drop wherever they go. Other ants can sense these perfumes and change their behavior based on them.
An experiment based on real-life harvesting ants showed that they always converged to the shortest path between the nest and the food source. Ants that have walked specific paths increased the pheromone intensity on those paths that other ants pick up on.
Ant colony optimization (ACO) algorithms simulate the emergent behavior shown in this experiment. In the case of finding the shortest path, the algorithm converges to a similar state, as observed with real ants. How can we use this to solve a more practical problem?
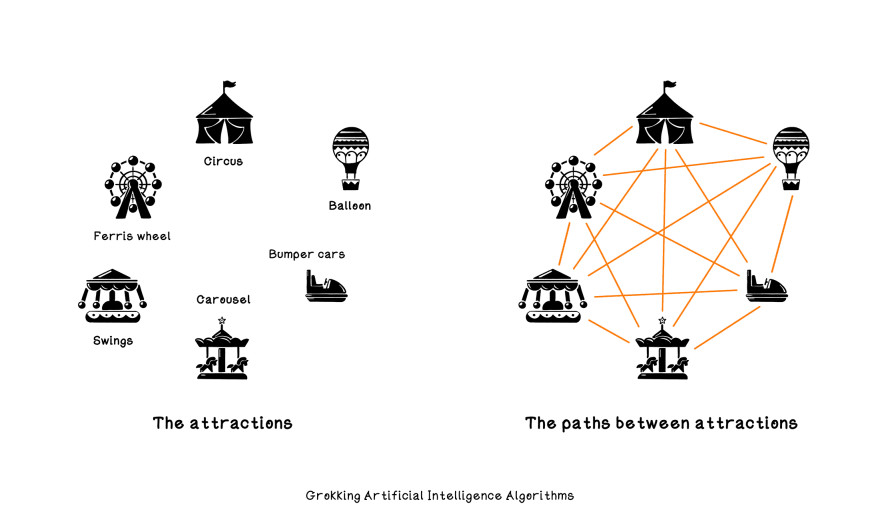
Imagine we're visiting a carnival that has many attractions to experience. Each attraction is located in a different area, with varying distances between them. Because we don’t feel like wasting time walking too much, we want to find the shortest paths between all attractions.
Ant colony optimization can help in finding the shortest path between all the attractions in a more computationally efficient way. If we represent an ant's memory, best distance, and actions it can take, we can simulate a colony and solve hard problems.
Follow for the next part to this thread - @RishalHurbans. To learn the details of this algorithm, see Grokking AI Algorithms with Manning Publications: http://bit.ly/gaia-book, or join my mailing list for infrequent knowledge drops: https://rhurbans.com/subscribe.







Top comments (0)