Median of Two Sorted Arrays

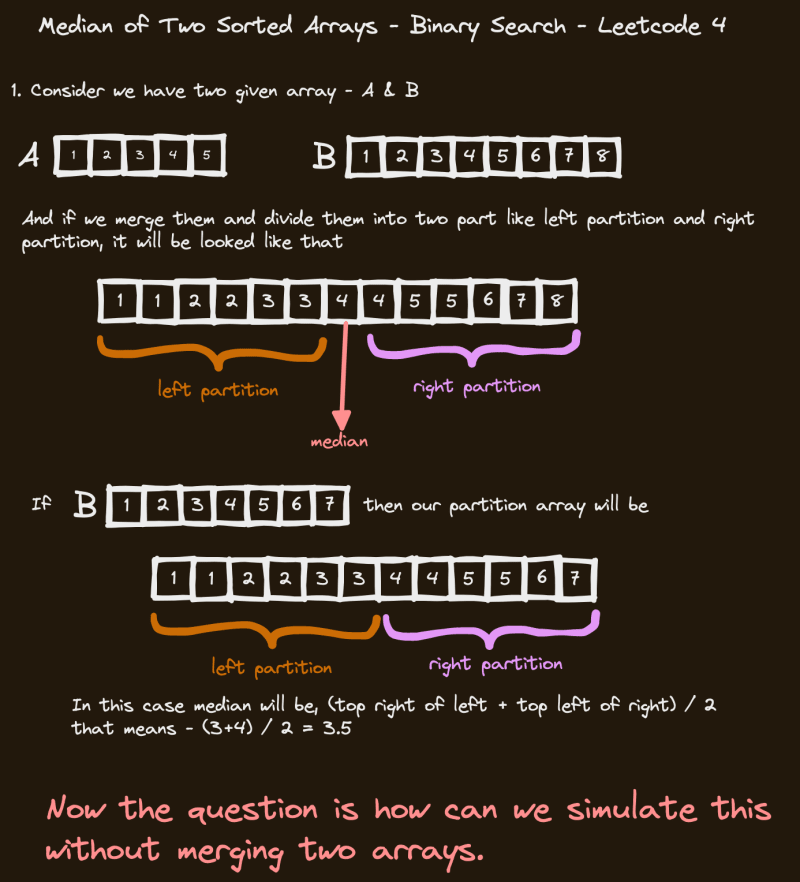
It's a very easy problem if we ignore the time complexity condition. Merge the two arrays, sort it and return the middle element if the merged array length is odd. And if the merged array length is even, add two middle elements and divide it by 2 and return the result.

But we should maintain the logarithmic time complexity, e.g: O(log(m+n))

So we should use any algorithm or technique that gives us logarithmic time complexity. And that is none other than Binary Search!

/**
 * @param {number[]} nums1
 * @param {number[]} nums2
 * @return {number}
 */
var findMedianSortedArrays = function(nums1, nums2) {
    let [a, b] = [nums1, nums2]
    const total = nums1.length + nums2.length
    const half = Math.floor(total/2) 

    if (a.length > b.length) {
        [a, b] = [nums2, nums1] 
        // we always do binary search in the smaller array which gives us time complexity O(log(min(m, n)))
    }

    let [left, right] = [0, a.length - 1]

    while(true) {
        let middleOfA = Math.floor((left + right) / 2)
        let middleOfB = half - middleOfA - 2 

        /*
        In left partition, if middle value is not found - that means middle index is less than 0(zero).
        That's why we are using -Infinity in this case.
        And vice-versa in the right partition.
        */
        let aLeft = a[middleOfA] !== undefined ? a[middleOfA] : -Infinity
        let aRight = a[middleOfA + 1] !== undefined ? a[middleOfA + 1] : Infinity
        let bLeft = b[middleOfB] !== undefined ? b[middleOfB] : -Infinity
        let bRight = b[middleOfB + 1] !== undefined ? b[middleOfB + 1] : Infinity

        if (aLeft <= bRight && bLeft <= aRight) {
            // that means our partition is correct
            if (total % 2 !== 0) return Math.min(aRight, bRight)
            else return (Math.max(aLeft, bLeft) + Math.min(aRight, bRight)) / 2 || 0.00
        } else if (aLeft > bRight) {
            // so we need to reduce the size of aLeft
            right = middleOfA - 1
        }else { 
            // bLeft > aRight, increase the size of aLeft
            left = middleOfA + 1
        }
    }
};