230. Kth Smallest Element in a BST 🚀

Solution Developed In:

The Question

For this article we will be covering Leetcode '230. Kth Smallest Element in a BST' question. This question is rated as a Medium question.

Question:

Given the root of a binary search tree, and an integer k, return the kth smallest value (1-indexed) of all the values of the nodes in the tree.

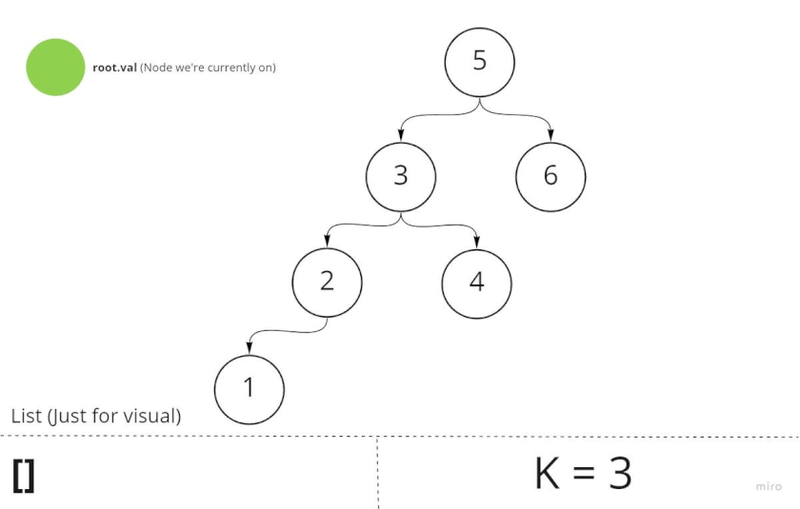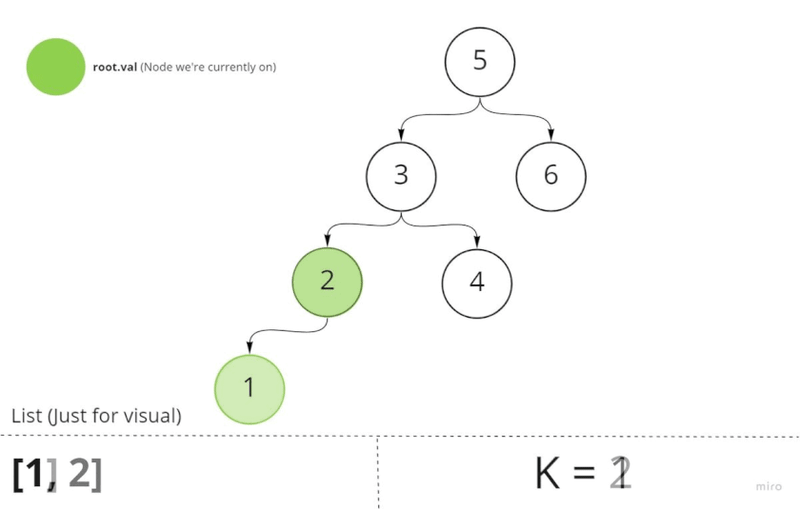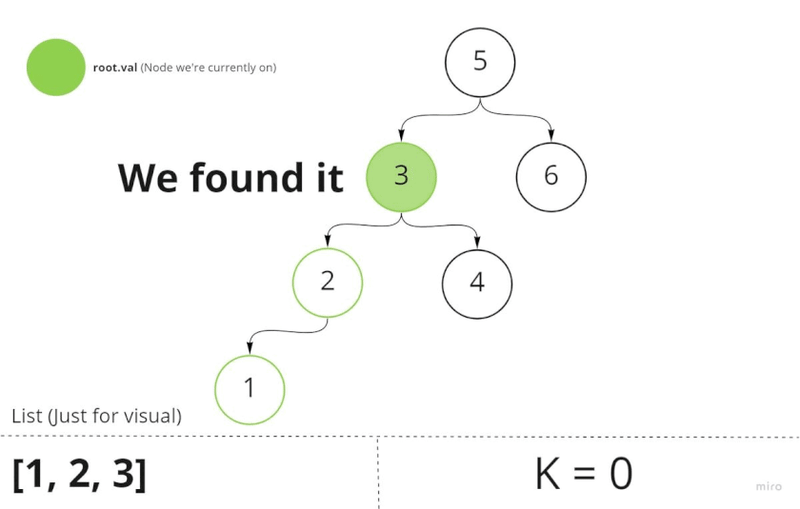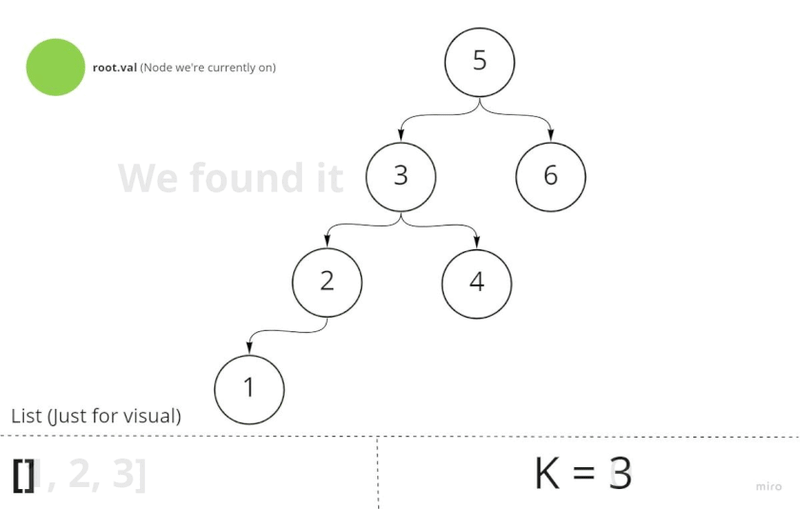
Example:

     3
    / \
   1   4
    \
     2

Input: root = [3,1,4,null,2], k = 1
Output: 1

Explaining The Question

This Question is rated Medium. Which I believe is accurate.

What the question is asking us to do is find the k smallest element. So if k is 1, then we need to find the smallest element in the BST. If k is 2, then we need to find the second smallest element in the BST.

Now we know that we're dealing with a Binary Search Tree so this mean's the smallest element will always be the left most element in the BST. So we can use a In-Order Traversal to find the absolutes smallest element.

The issue with this is that, k could potentially be the last node in the BST. So what we know is that we're going to use some form of traversal to traverse the entire tree. As we may have to do that.

As we're in a BST we can use Depth First Search In-Order traversal, it should present you an array of values in sorted order. Which is a neat little trick for traversing a BST in ascending order. Meaning we go from the smallest element to the greatest element.

Now you can traverse the BST and store it within a stack. Then just return the k element of that stack. But this would reduce the average time and space complexity of our algorithm. We're going to play it smart and just go to the k node in the BST and return that. Meaning, that our space complexity will be better and so will our time complexity.

Recommended Knowledge

1. Binary Tree
2. Depth First Search
3. In-order traversal
4. Binary Search Tree
5. Recursion

What do we know?

1. We have been given a Binary Search Tree and an integer k.
2. We need to find the k smallest element in the BST.
3. We're using a Binary Search Tree. So we can use a Depth First Search In-Order traversal to traverse the BST in ascending order.
4. Given the In-Order Traversal, we can traverse k nodes in the BST. Which is the same as the k smallest element in the BST.

How we're going to do it:

The solution to this problem is to use a Depth First Search In-Order traversal to traverse the BST in ascending order. What this mean's is that once we have traversed k nodes in the BST, we can return the value of the node.

That makes no sense?!?!

I know, I know, I know. It didn't make sense to me either. It was only until I did the Recover Binary Search Tree that it eventually made sense.

Think of it like this, when you perform in-order traversal on a BST, you're going to traverse the BST in ascending order. Meaning you start at the smallest element and go to the greatest element. Like this:
[1,2,3,4,5,6,7,8,9]. Think of it like a sorted array.

Given this information, all we have to is move k nodes using in-order traversal. This would land us on the k node. At this point, all we have to is return it.

1. Declare a global flag to keep track of the return result. Which will be the value of the k nodes. This just makes our lives easier
2. Perform a Depth First Search In-Order traversal to traverse the BST in ascending order.
3. Each time we move a node, we will decrement the k value. So, K-=1 until we reach the k node (k === 1). Meaning we're now on the k node. Here we set the global flag to the value of the k node.
4. Return that value anywhere.

Big O Notation:

• Time Complexity: O(n) | Where n is the number of nodes in our Binary Search Tree | As in the worst case scenario, we're going to traverse the entire BST. As K will be the number of nodes in the BST.
• Space Complexity: O(h) | Where h is the height of the Binary Search Tree | Because we're going to store the height of the tree within the Call Stack due to the in-order traversal.

'Could this be improved?' Yes! Morris Traversal could do this problem in O(1) space complexity. But Morris Traversal is tricky and tough to read. For the sake of simplicity, I don't use it here.

Leetcode Results:

See Submission Link:

• Runtime: 89 ms, faster than 44.57% of JavaScript online submissions for Kth Smallest Element in a BST.
• Memory Usage: 48.1 MB, less than 89.49% of JavaScript online submissions for Kth Smallest Element in a BST

---

The Solution

var kthSmallest = function (root, k) {



    // This is what is ultimately returned in the end
    // This is also used as a flag to let our in-order traversal know when to stop / stop traversing
    let return_result = null;

    // We're going to traverse the BST in-order
    // Why? Well, we want to find the kth smallest element, correct?
    // One of the cool tricks about a BST is that it's a sorted tree
    // So if you traverse the tree 'in-order' you'll always start at the smallest element
    // then to the second smallest, then third smallest, etc.
    // Try it out! Slap a console.log in the middle of the in-order traversal to see what it does
    const in_order_traversal = (node) => {

        // So, we have either reached the end of the tree or we have found the kth smallest element
        if (!node || return_result) {
            return return_result;
        }

        // Traverse the left subtree
        in_order_traversal(node.left);

        // So, k === 1, meaning, we're now on 
        // the desired node and as to not repeat
        // the same node, we'll check that the return_result
        // hasn't already been set
        if (k === 1 && return_result === null) {

            // Set the return result to the current nodes value
            // as this node is the kth smallest element
            return_result = node.val;

            // Also return it. As to stop the in-order traversal
            return return_result;
        } else {

            // So, we're not on the desired node
            // Decrement by 1. 
            k -= 1;
        }

        // Traverse the right subtree
        in_order_traversal(node.right);

        // Return the result
        return return_result;
    };

    return in_order_traversal(root);
};