Machine Learning
หากพูดถึงการทำเรียนรู้ด้วยเครื่องจักร (Machine Learning) แล้วกระบวนการหนึ่งที่เราต้องทำคือการปรับปรุงประสิทธิภาพ (optimzation ) ของโมเดล ซึ่งวิธีการหนึ่งที่ถูกนำมาใช้เพื่อช่วยปรับปรุงโมเดลคือ Gradient descent นั้นเอง
Regression
หากเรามีข้อมูลชุดหนึ่งซึ่งแสดงความสัมพันธ์ระหว่างดัช BMI กับค่ารักษาค่ารักษาพยาบาล เป็นดังตารางนี้
bmi | charges
1 33.00 | 4449.460
2 28.88 | 3866.850
3 25.74 | 3756.621
4 33.44 | 8240.589
5 27.74 | 7281.505
6 29.83 | 6406.410
7 30.78 | 10797.336
8 40.30 | 10602.380
9 32.40 | 4149.730
10 28.02 | 6203.900
11 28.60 | 4687.790
12 26.60 | 3046.060
13 36.63 | 4949.758
14 21.78 | 6272.477
15 30.80 | 6313.750
เราสามารถนำมาพลอตกราฟเพื่อดูความสัมพันธ์ของข้อมูลได้ดังภาพด้านล่าง ซึ่งเมื่อดูจากจุดที่พลอตแล้ว เราก็ตัดสินใจว่าจะใช้สมการเส้นตรงเพื่ออธิบายความสัมพันธ์ของตัวแปรสองตัวนี้:
โดยสมการเส้นตรงมีสูตรดังนี้
y = θ₀+θ₁x
θ₀ เป็นระยะตัดแกน y (intercept)
θ₁ เป็นความชันของเส้นตรง
หากเราลากเส้นตรงสามเส้นเราจะทราบได้อย่างไรว่าเส้นตรงเส้นไหนให้ผลลัพธ์ที่ดีกว่ากัน หากเราจะนำฟังก์ชันของเส้นตรงนี้มาเป็นโมเดลในการพยากรณ์ค่ารักพยาบาลที่ต้องจ่าย โดยคำณวนค่ารักษาพยาบาลที่คาดว่าจะต้องจ่ายจากดัชนี BMI เราจะได้ว่า f(x) = y ซึ่ง f(x) ก็คือโมเดลเรานั่นเอง
Optimization
ใน machine learning เมื่อเราได้สมการหรือฟังก์ชันที่ต้องการหาคำตอบแล้วมาแล้ว เราต้องมาทำการหาค่าพารามิเตอร์เพื่อให้โมเดลหรือสมการที่ได้มีค่าความผิดพลาดน้อยที่สุด จากตัวอย่างฟังชันก์แสดงความสัมพันธ์ระหว่างดัชนี BMI กับค่ารักษาค่ารักษาพยาบาล เราจะได้สมการเป็น f(x) = θ₀+θ₁x , x=ดัชนี bmi
ซึ่งสิ่งที่เราต้องหาคือค่า θ₀ และ θ₁ ที่ใช้สำหรับสร้างเส้นตรงที่เมื่อเราแทน x เข้าไปแล้วให้ผลลัพธ์(y)ที่ใกล้เคียงค่าจริงมากที่สุด โดยอัลกอริทึมหนึ่งที่นิยมใช้หาค่าเหล่านี้ (minimize cost function) ก็คือ Gradient Descent นั้นเอง
Gradient Descent
หลักการทำงานของ Gradient Descent สามารถเขียนเป็นสมการทางคณิตศาสตร์ได้ดังนี้
θ = θ − α · ∇θJ(θ)
α คือ Learning Rate
J(θ) คือฟังก์ชันที่ใช้ในการประเมินผล (Cost/Loss function)

ที่มา https://developers.google.com/machine-learning/crash-course/reducing-loss/gradient-descent
โดยอย่างที่ทราบกันว่าเราสามารถใช้อนุพันธ์ในการหาจุดต่ำสุดหรือจุดสูงสุดได้ ซึ่งจุดต่ำสุดก็คือจุดที่เราต้องการนั้นเอง ดังนั้น Gradient Descent จึงใช้หลักการนี้ในการหาค่าที่ให้เออเรอร์น้อยที่สุด
Learning Rate
อัตราการเรียนรู้เป็นตัวเลขที่เปรียบเสมือนขนาดของก้าวแต่ละก้าวที่จะเดิน เพื่อไปให้ถึงก้นหลุม หากเราก้าวยาวไปก็จะเดินข้ามก้นหลุม แต่หากก้าวสั้นไปก็จะใช้เวลานาน ตามภาพด้านล่าง
Cost function/Lost function
เป็นฟังก์ชันที่เอาไว้สำหรับประเมินว่าฟังก์ชันที่ได้มีความแม่นยำมากน้อยเพียงใด เช่น sum of square error หรือ
หลัก ๆ แล้ว gradient descent แบ่งได้เป็น 3 แบบ
- Batch gradient descent
- Stochastic gradient descent
- Mini batch gradient descent
Batch Gradient Descent
หลักการของ Batch Gradient Descent คือ นำค่าที่ได้จากรอบเก่ามาคำนวณหาผลลัพธ์ในรอบถัดไป โดยนำข้อทุกชุดมาคำนวณ
ตัวอย่างการทำคำนวณจากตาราง หากต้องการหาค่า θ₀ และ θ₁จะได้ว่า
Hypothesis: h(x) = θ₀–θ₁x
Cost function: J(θ₀, θ₁) = Σ(h(xᵏ)-yᵏ)²
Gradient calculation: θj = θj - α * 1⁄m * Σ(hθ(x(i)) - y(i)) * x(i)
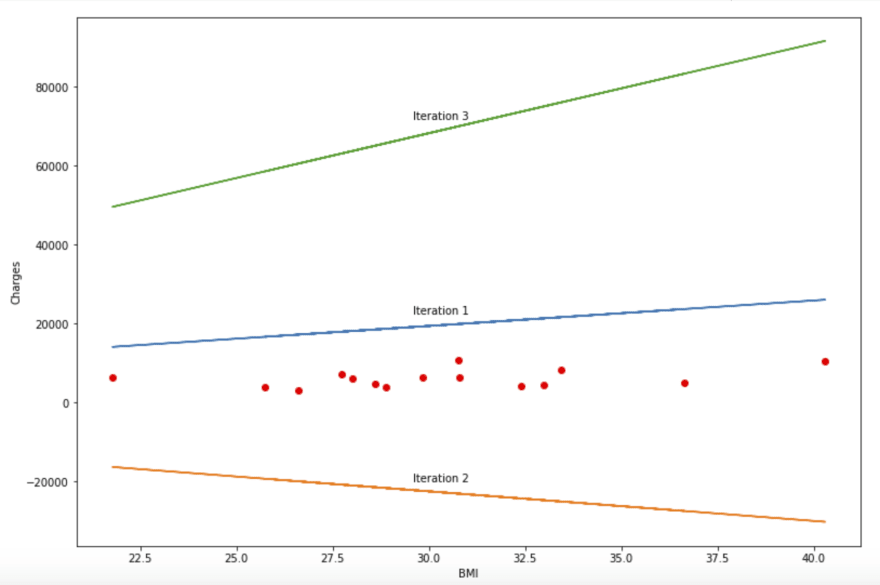
ซึ่งหากเราทำการคำนวณโดยให้ค่าเริ่มต้นเป็นดังนี้ θ₀=1, θ₁=1, ⍺=0.0015 โดยคำนวณทั้งหมด 3 ครั้ง เราจะได้ผลลัพธ์ในดังนี้
Iteration 1
Theta 0: 1 - 0.0015 * 0.1 * [
(1 + 33.00 - 4449.46) + (1 + 28.88 - 3866.85) +
(1 + 25.74 - 3756.62) + (1 + 33.44 - 8240.59) +
(1 + 27.74 - 7281.51) + (1 + 29.83 - 6406.41) +
(1 + 30.78 - 10797.34) + (1 + 40.30 - 10602.38) +
(1 + 32.40 - 4149.73) + (1 + 28.02 - 6203.90) +
(1 + 28.60 - 4687.79) + (1 + 26.60 - 3046.06) +
(1 + 36.63 - 4949.76) + (1 + 21.78 - 6272.48) +
(1 + 30.80 - 6313.75) ]
Theta 1: 1 - 0.0015 * 0.1 * [
(1 + 33.00 - 4449.46) * 33.00 + (1 + 28.88 - 3866.85) * 28.88 +
(1 + 25.74 - 3756.62) * 25.74 + (1 + 33.44 - 8240.59) * 33.44 +
(1 + 27.74 - 7281.51) * 27.74 + (1 + 29.83 - 6406.41) * 29.83 +
(1 + 30.78 - 10797.34) * 30.78 + (1 + 40.30 - 10602.38) * 40.30 +
(1 + 32.40 - 4149.73) * 32.40 + (1 + 28.02 - 6203.90) * 28.02 +
(1 + 28.60 - 4687.79) * 28.60 + (1 + 26.60 - 3046.06) * 26.60 +
(1 + 36.63 - 4949.76) * 36.63 + (1 + 21.78 - 6272.48) * 21.78 +
(1 + 30.80 - 6313.75) * 30.80 ]
Theta θ₀=10.06, θ₁=281.47
Iteration 2
Theta 0: 10.06 - 0.0015 * 0.1 * [
(10.06 + 9288.51 - 4449.46) + (10.06 + 8128.85 - 3866.85) +
(10.06 + 7245.04 - 3756.62) + (10.06 + 9412.36 - 8240.59) +
(10.06 + 7807.98 - 7281.51) + (10.06 + 8396.25 - 6406.41) +
(10.06 + 8663.65 - 10797.34) + (10.06 + 11343.24 - 10602.38) +
(10.06 + 9119.63 - 4149.73) + (10.06 + 7886.79 - 6203.90) +
(10.06 + 8050.04 - 4687.79) + (10.06 + 7487.10 - 3046.06) +
(10.06 + 10310.25 - 4949.76) + (10.06 + 6130.42 - 6272.48) +
(10.06 + 8669.28 - 6313.75) ]
Theta 1: 281.47 - 0.0015 * 0.1 * [
(10.06 + 9288.51 - 4449.46) * 33.00 + (10.06 + 8128.85 - 3866.85) * 28.88 +
(10.06 + 7245.04 - 3756.62) * 25.74 + (10.06 + 9412.36 - 8240.59) * 33.44 +
(10.06 + 7807.98 - 7281.51) * 27.74 + (10.06 + 8396.25 - 6406.41) * 29.83 +
(10.06 + 8663.65 - 10797.34) * 30.78 + (10.06 + 11343.24 - 10602.38) * 40.30 +
(10.06 + 9119.63 - 4149.73) * 32.40 + (10.06 + 7886.79 - 6203.90) * 28.02 +
(10.06 + 8050.04 - 4687.79) * 28.60 + (10.06 + 7487.10 - 3046.06) * 26.60 +
(10.06 + 10310.25 - 4949.76) * 36.63 + (10.06 + 6130.42 - 6272.48) * 21.78 +
(10.06 + 8669.28 - 6313.75) * 30.80 ]
Theta θ₀=6.35, θ₁=167.2
Iteration 3
Theta 0: 6.35 - 0.0015 * 0.1 * [
(6.35 + 5517.60 - 4449.46) + (6.35 + 4828.74 - 3866.85) +
(6.35 + 4303.73 - 3756.62) + (6.35 + 5591.17 - 8240.59) +
(6.35 + 4638.13 - 7281.51) + (6.35 + 4987.58 - 6406.41) +
(6.35 + 5146.42 - 10797.34) + (6.35 + 6738.16 - 10602.38) +
(6.35 + 5417.28 - 4149.73) + (6.35 + 4684.94 - 6203.90) +
(6.35 + 4781.92 - 4687.79) + (6.35 + 4447.52 - 3046.06) +
(6.35 + 6124.54 - 4949.76) + (6.35 + 3641.62 - 6272.48) +
(6.35 + 5149.76 - 6313.75) ]
Theta 1: 167.2 - 0.0015 * 0.1 * [
(6.35 + 5517.60 - 4449.46) * 33.00 + (6.35 + 4828.74 - 3866.85) * 28.88 +
(6.35 + 4303.73 - 3756.62) * 25.74 + (6.35 + 5591.17 - 8240.59) * 33.44 +
(6.35 + 4638.13 - 7281.51) * 27.74 + (6.35 + 4987.58 - 6406.41) * 29.83 +
(6.35 + 5146.42 - 10797.34) * 30.78 + (6.35 + 6738.16 - 10602.38) * 40.30 +
(6.35 + 5417.28 - 4149.73) * 32.40 + (6.35 + 4684.94 - 6203.90) * 28.02 +
(6.35 + 4781.92 - 4687.79) * 28.60 + (6.35 + 4447.52 - 3046.06) * 26.60 +
(6.35 + 6124.54 - 4949.76) * 36.63 + (6.35 + 3641.62 - 6272.48) * 21.78 +
(6.35 + 5149.76 - 6313.75) * 30.80 ]
Theta θ₀=7.84, θ₁=213.76
ซึ่งเมื่อผ่านไป 3 ครั้งสมการที่เราจะได้เพื่อเป็นโมเดลคือ
y = 7.84 + 213.76x , โดยที่ x เป็นดัชนี bmi และ y เป็นค่ารักษาพยาบาล
ซึ่งเมื่อนำมาพลอ๊ตกราฟจะได้ดังรูปด้านล่าง
Stochastic Gradient Descent
เนื่องจาก Batch gradient descent จะต้องนำข้อมูลทุกชุดมาคำนวณในแต่ละรอบ ทำให้ใช้เวลาในการคำนวณนาน Stochastic จึงถือกำเนิดขึ้นมาเพื่อลดเวลาในการประมวลผล การทำงานของ Stochastic gradient descent จะเหมือนกับ Batch เพัยงแต่ในแต่ละรอบจะสุ่มข้อมูลเพียงชุดเดียวมาทำการคำนวณ
Hypothesis: h(x) = θ₀–θ₁x
Cost function: J(θ₀, θ₁) = Σ(h(xᵏ)-yᵏ)²
Gradient calculation: θj = θj - α * 1⁄m * (hθ(x(i)) - y(i)) * x(i)
ซึ่งหากเราทำการคำนวณโดยให้ค่าเริ่มต้นเป็นดังนี้ θ₀=1, θ₁=1, ⍺=0.0015 โดยคำนวณทั้งหมด 3 ครั้ง เราจะได้ผลลัพธ์ในดังนี้
Iteration 1 Choose row : 3
Theta 0: 1 - 0.0015 * 0.1 * [(1 + 25.74 - 3756.62) ]
Theta 1: 1 - 0.0015 * 0.1 * [(1 + 25.74 - 3756.62) * 25.74 ]
Theta θ₀=1.37, θ₁=10.6
Iteration 2 Choose row : 1
Theta 0: 1.37 - 0.0015 * 0.1 * [(1.37 + 349.80 - 4449.46) ]
Theta 1: 10.6 - 0.0015 * 0.1 * [(1.37 + 349.80 - 4449.46) * 33.00 ]
Theta θ₀=1.78, θ₁=24.12
Iteration 3 Choose row : 4
Theta 0: 1.78 - 0.0015 * 0.1 * [(1.78 + 806.57 - 8240.59) ]
Theta 1: 24.12 - 0.0015 * 0.1 * [(1.78 + 806.57 - 8240.59) * 33.44 ]
Theta θ₀=2.52, θ₁=48.97
จะสังเกตุได้ว่าเส้นที่ลากของ Stochastic ไม่ดีเท่า Batch ที่เป็นเช่นนี้เพราะใช้ข้อมูลเพียงชุดเดียวในการทำงานแต่ละรอบนั้นเอง ถ้าปล่อยให้รันไปเรื่อย ๆ 15 รอบจะได้ดังนี้
จากภาพจะเห็นว่าค่าเข้าใกล้จุดที่เหมาะสมขึ้นเรื่อย ๆ
หรือหากเปลี่ยน learning rate เป็นค่าต่าง ๆ ดังนี้
| α = 0.01 | α = 0.03 | α = 0.05 |
|---|---|---|
 |
 |
 |
จากผลลัพธ์ที่ได้ พบว่าการปรับ Learning Rate ให้อยู่ในค่าที่เหมาสะสมมีผลต่อระยะเวลาในการเรียนรู้มากทีเดียว
Mini batch Gradient Descent
จะเห็นได้ว่า Stochastic แม้จะใช้เวลาสั้นแต่ในการเรียนรู้แต่ละรอบก็ไม่ค่อยเสถียร Mini batch จึงเกิดขึ้นเพื่อนำข้อดีของแต่ละวิธีมารวมกันนั้นเอง โดยแทนที่จะคำนวณข้อมูลทุกชุดแบบ Batch หรือเพียงชุดเดียวแบบ Stochastic Mini batch จะทำการคำนวณแต่ละรอบโดยใช้ข้อมูลจำนวน b ชุด
Hypothesis: h(x) = θ₀–θ₁x
Cost function: J(θ₀, θ₁) = Σ(h(xᵏ)-yᵏ)²
Gradient calculation: θj = θj - α * 1⁄m * Σ(hθ(x(i)) - y(i)) * x(i)
ซึ่งหากเราทำการคำนวณโดยให้ค่าเริ่มต้นเป็นดังนี้ θ₀=1, θ₁=1, ⍺=0.0015, 3 โดยคำนวณทั้งหมด 3 ครั้ง เราจะได้ผลลัพธ์ในดังนี้
Iteration 1 selected row 14-11
Theta 0: 1 - 0.0015 * 0.1 * [
(1 + 21.78 - 6272.48) +
(1 + 32.40 - 4149.73) +
(1 + 28.60 - 4687.79) ]
Theta 1: 1 - 0.0015 * 0.1 * [
(1 + 21.78 - 6272.48) * 21.78 +
(1 + 32.40 - 4149.73) * 32.40 +
(1 + 28.60 - 4687.79) * 28.60 ]
Theta θ₀=2.5, θ₁=41.27
Iteration 2 selected row 3-12
Theta 0: 2.5 - 0.0015 * 0.1 * [
(2.5 + 1062.29 - 3756.62) +
(2.5 + 1231.08 - 6406.41) +
(2.5 + 1097.78 - 3046.06) ]
Theta 1: 41.27 - 0.0015 * 0.1 * [
(2.5 + 1062.29 - 3756.62) * 25.74 +
(2.5 + 1231.08 - 6406.41) * 29.83 +
(2.5 + 1097.78 - 3046.06) * 26.60 ]
Theta θ₀=3.48, θ₁=68.81
Iteration 3 selected row 9-8
Theta 0: 3.48 - 0.0015 * 0.1 * [
(3.48 + 2229.44 - 4149.73) +
(3.48 + 2301.01 - 8240.59) +
(3.48 + 2773.04 - 10602.38) ]
Theta 1: 68.81 - 0.0015 * 0.1 * [
(3.48 + 2229.44 - 4149.73) * 32.40 +
(3.48 + 2301.01 - 8240.59) * 33.44 +
(3.48 + 2773.04 - 10602.38) * 40.30 ]
Theta θ₀=5.05, θ₁=126.41
ซึ่งสามารถวาดกราฟได้ดังนี้
Summary
Gradient Descent เป็นวิธีการหนึ่งในการทำ Optimization สำหรับ Model โดยหลัก ๆ มีอยู่ 3 แบบแต่ละแบบมีข้อดีและข้อเสียแตกต่างกันไป
Batch เสถียรแต่ช้า
Stochastic เร็วแต่ไม่ค่อยเสถียร
Mini batch นำข้อดีมารวมกันแต่ก็ไปไม่สุดในด้านใดด้านหนึ่ง
ครั้งหน้าเราจะนำ Linear Regression และ Gradient descent ไปช่วยในการสร้างโมเดลเพื่อพยากรณ์ราคาบ้านกัน










Top comments (0)