Binary Search Trees (BTS) are an extremely useful data structure found in a variety of applications. They provide O(log^n) time complexity for most operations. However, when a tree becomes unbalanced (IE. too many entries on the left or the right of a given node), the time complexity of operations degrade to something that looks more like a linked list. Several self-balancing tree data structures exist to solve this problem. These solutions can be found in anything from LSM Tree based databases (Cassandra, Hbase, RocksDB, etc) to the Completely Fair Scheduler algorithm that is used in the Linux Kernel as the default processes scheduling algorithm. This tutorial will cover the implementation of a particular self-balancing tree known as a Red-Black Tree in Golang.
Overview
Red Black Tree's have constraints that guaranty relative (tho not perfect) balance on both sides. Those constraints are:
- The Root node is always Black
- All leaf nodes are black
- There can be no adjacent red nodes. (IE red node will have two black children nodes)
- Every simple path from a node to a descendant leaf contains the same number of black nodes.
These constraints guarantee that a tree will be relatively balanced. These constraints are maintained on every mutation by a combination of re-coloring and node rotations based on other node relationships (Parent, Grand Parent, Siblings, etc). Today we will be developing the parts of the Red-Black Tree to handle insertions. This tutorial assumes a working knowledge of BST trees.
Implementation
It's important to realize a red-black tree is still a BST. This means insertions and searches are handled in the same way as with a normal BST Tree. We can then implement the parts of a BST that we are familiar with.
The struct that represents our tree and public insertion related functions we know are on a BST Tree for consumers. Additionally, the red-black tree requires some private functions for tree correction and rotation:
// tree.go
package tree
import (
"fmt"
)
type RedBlackTree struct {
Root *Node
}
func (*r RedBlackTree) Insert(node *RedBlackNode) {}
func (*r RedBlackTree) Search(key string) *RedBlackNode {}
func (*r RedBlackTree) fixTreeAfterInsertion(node *RedBlackNode) {}
func (*r RedBlackTree) rotateLeft(node *RedBlackNode) {}
func (*r RedBlackTree) rotateRight(node *RedBlackNode) {}
Next, we will define our Node, a new property called Color to represent whether a node is red or black, and the Node’s Parent. Additionally, we will define a NilNode for leaf nodes:
// tree.go
type Color uint
const (
RED Color = iota
BLACK
)
type RedBlackNode struct {
Color Color
Key string
Parent *RedBlackNode
Left *RedBlackNode
Right *RedBlackNode
}
var NilNode = &RedBlackNode{Color: BLACK}
Now that we have the structure lets implement some functions:
BST Insertion and Search
Insertion is just a BST insertion at first so let us implement that function as we know how. Take notice that the fixTreeAfterAdd function gets called on every insertion. So, we'll add that too, though it's just a no-op right now:
// tree.go
func (r *RBTree) Insert(node *RedBlackNode) {
if r.Root == nil {
r.Root = node
} else {
currentNode := r.Root
for {
if node.Key == currentNode.Key {
return // Do nothing as node already in tree
}
if node.Key > currentNode.Key {
if currentNode.Right == NilNode {
node.Parent = currentNode
currentNode.Right = node
break
}
currentNode = currentNode.Right
}
if node.Key < currentNode.Key {
if currentNode.Left == NilNode {
node.Parent = currentNode
currentNode.Left = node
break
}
currentNode = currentNode.Left
}
}
r.fixTreeAfterAdd(node) // No-Op right now
}
}
Now let us write a test to assert correctness so far. I use a technique from property based testing that involves generating a lot of random input for my tree. I use the helper methods func String(length int) string and StringWithCharset(length int, charset string) string to generate this input:
// tree_test.go
package tree_test
import (
"math/rand"
"sort"
"testing"
"time"
. "github.com/srleyva/LSM/pkg/trees"
)
func TestRBTress(t *testing.T) {
// Generate List
entryCount := 10000
entries := make([]string, entryCount)
for i := 0; i < entryCount; i++ {
entries[i] = String(10)
}
t.Run("Test insertion into an RB Tree", func(t *testing.T) {
// Set Up tree
tree := &RedBlackTree{nil}
for _, entry := range entries {
newNode := &RedBlackNode{
Color: Black,
Key: entry,
Parent: NilNode,
Right: NilNode,
Left: NilNode
}
tree.Insert(newNode)
}
})
}
func String(length int) string {
return StringWithCharset(length, charset)
}
func StringWithCharset(length int, charset string) string {
b := make([]byte, length)
for i := range b {
b[i] = charset[seededRand.Intn(len(charset))]
}
return string(b)
}
At the moment, this doesn't test for anything but sets up the necessary scaffolding we need for testing. We now need a function to retrieve our key, so let us add that. Once again, this is just a classic BST Search and quite similar to the Insertion Algorithm.
// tree.go
...
func (*r RedBlackTree) Search(key string) *RedBlackNode {
currentNode := r.Root
for currentNode != NilNode && key != currentNode.Key {
if key < currentNode.Key {
currentNode = currentNode.Left
}
if key > currentNode.Key {
currentNode = currentNode.Right
}
}
if currentNode == NilNode {
return nil, fmt.Errorf("key does not exist in tree: %s", key)
}
return currentNode, nil
}
Now we can modify out test:
func TestRBTress(t *testing.T) {
// Generate List
entryCount := 10000
entries := make([]string, entryCount)
for i := 0; i < entryCount; i++ {
entries[i] = String(10)
}
t.Run("Test insertion and retrieval on RB Tree", func(t *testing.T) {
// Set Up tree
tree := &RedBlackTree{nil}
for _, entry := range entries {
newNode := &RedBlackNode{
Color: Black,
Key: entry,
Parent: NilNode,
Right: NilNode,
Left: NilNode
}
tree.Insert(newNode)
}
// Pick random entry for entry list
randomIndex := rand.Intn(entryCount)
entry, err := tree.Search(entries[randomIndex])
if err != nil {
t.Errorf("err where not expected: %s", err)
}
if entry.Key != entries[randomIndex] {
t.Errorf("search returned incorrect key: got=[%d] expected=[%d]", entry.Key, entries[randomIndex])
}
})
}
Now we run that test and see it is passing
go test -timeout 30s
# Output
ok github.com/srleyva/LSM/pkg/trees
Success: Tests passed.
Now, let us add a specific test to check for RedBlackTree level constrains. Also, I am adding a helper function to calculate the height constraint.
Now I am not going to conflate unit testing methodology here as that's a topic for another day, for simplicity I will keep all my tests in one case, though if this were a production product, I would not ship with this test:
// tree_test.go
...
t.Run("Test RB Tree", func(t *testing.T) {
// Set Up tree
tree := &RedBlackTree{nil}
for _, entry := range entries {
newNode := &RedBlackNode{
Color: Black,
Key: entry,
Parent: NilNode,
Right: NilNode,
Left: NilNode
}
tree.Insert(newNode)
}
// Pick random entry for entry list
randomIndex := rand.Intn(entryCount)
entry, err := tree.Search(entries[randomIndex])
if err != nil {
t.Errorf("err where not expected: %s", err)
}
if entry.Key != entries[randomIndex] {
t.Errorf("search returned incorrect key: got=[%d] expected=[%d]", entry.Key, entries[randomIndex])
}
// Test Height Constraint
maxHeight := 2 * LogN(entryCount+1)
node := tree.Root
count := 0
for node != NilNode {
count++
node = node.Right
}
if count > maxHeight+1 {
t.Errorf("Broke Level Contraints: got=[%d] expected=[less than %d]", count, maxHeight+1)
}
})
...
func LogN(n int) int {
if n < 1 {
return 0
}
return 1 + LogN(n/2)
}
Running will yield an error about height constraints, as we have not implemented the balancing but right now we have a basic BST Insertion and Search Algorithm.
Perfectly Balanced (though not really), as all things should be.
So we know that red-black trees involve re-coloring and node rotations in that order. First, re-coloring will attempt to adjust the tree to satisfy the Red-Black Tree Constraints. If re-coloring does not work, then the algorithm will perform node rotations to fix the tree.
Rotations
Let's implement rotations first as they are the last in the order of operation for Red Black Trees after re-coloring.
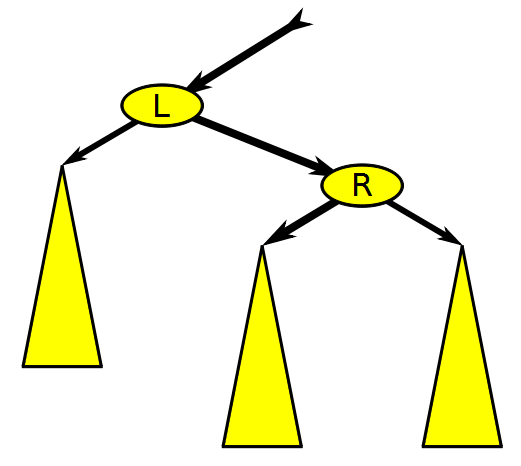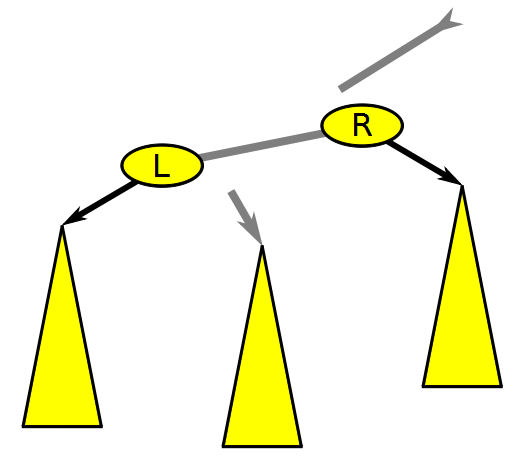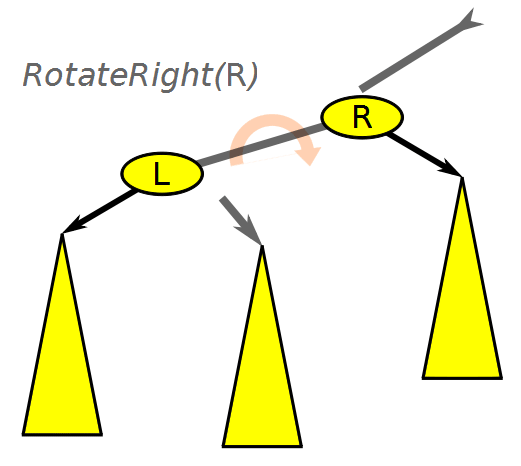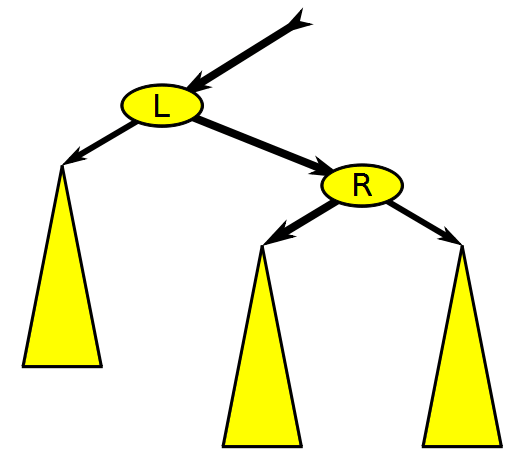
First, an animation to demonstrate rotations:
Notice how the BST properties are maintained. For example, a left rotation will shift a child node to the parent, however, the children to the left of the child node being promoted are now moved to a right child under the old parent. This is because these children are greater than the old parent but still less than the new parent.
Here is the implementation
// tree.go
func (r *RBTree) rotateLeft(node *RedBlackNode) {
// Right of node (old parent) will become the new parent
RightNode := node.Right
// Assign the right tree of new parent to old parent
node.Right = RightNode.Left
// Tell the right tree of new parent about the change by setting a new Parent Property
RightNode.Left.Parent = node
// Assign old parent's parent to new parent
RightNode.Parent = node.Parent
// Correct top of tree
// If this is the top of the tree
// Make RightNode root
if RightNode.Parent == nil {
r.Root = RightNode
}
// If This is not top of tree, need to fix node's parent node
// Check if node is Left or Right of Parent Node and assign RightNode
if node == node.Parent.Left {
node.Parent.Left = RightNode
}
if node == node.Parent.Right {
node.Parent.Right = RightNode
}
// Demote current parent to child of new parent
RightNode.Left = node
node.Parent = RightNode
}
The right rotation will be an inverse of the above logic:
// tree.go
func (r *RBTree) rotateRight(node *RedBlackNode) {
LeftNode := node.Left
node.Left = LeftNode.Right
LeftNode.Right.Parent = node
LeftNode.Parent = node.Parent
if LeftNode.Parent == nil {
r.Root = LeftNode
} else if node == node.Parent.Left {
node.Parent.Left = LeftNode
} else if node == node.Parent.Right {
node.Parent.Right = LeftNode
}
LeftNode.Right = node
node.Parent = LeftNode
}
Re-coloring
The next operation after the mutation (this case insertion) is a re-coloring. This is done to assert whether or not rotation is necessary. It is done after every insertion.
func (r *RBTree) fixTreeAfterAdd(node *RedBlackNode) {
node.Color = RED // New nodes are always red
// If node is root or the parent is Black, we don't need to perform any re-coloring
for node != r.Root && node.Parent.Color == RED {
// Check if parent is a right or left node
// If parent is left node
if node.Parent.Parent.Left == node.Parent {
// because parent is left of grandparent, uncle is right of grandparent
uncle := node.Parent.Parent.Right
// If uncle is red, recolor parent and uncle to black
if uncle.Color == RED {
// Recolor parent and uncle to black increasing the black node count from nth node to leaf by 1
node.Parent.Color = BLACK
uncle.Color = BLACK
// Make the granparent red
node.Parent.Parent.Color = RED
// Traverse up the tree to grandparent and re-run through fix algorithm
node = node.Parent.Parent
} else { // Uncle is black
// if node is a right child
if node == node.Parent.Right {
// traverse up to parent
node = node.Parent
// rotate left
r.rotateLeft(node)
}
// recolor parent to black
node.Parent.Color = BLACK
// recolor grandparent to red
node.Parent.Parent.Color = RED
// rotate grandparent right
r.rotateRight(node.Parent.Parent)
}
} else if node.Parent.Parent.Right == node.Parent {
// because parent is right of grandparent uncle is inverse left of grandparent
uncle := node.Parent.Parent.Left
// if uncle is read re-coloring is all thats needed
if uncle.Color == RED {
// increasing black node count to leaf from nth node to one
node.Parent.Color = BLACK
uncle.Color = BLACK
// traverse to grandparent and re-run fix algorithm
node = node.Parent.Parent
} else { // unlce is black, rotation is needed
if node == node.Parent.Left {
// traverse to parent
node = node.Parent
// rotate right
r.rotateRight(node)
}
// recolor parent to black
node.Parent.Color = BLACK
// recolor grandparent to red
node.Parent.Parent.Color = RED
// rotate left
r.rotateLeft(node.Parent.Parent)
}
}
}
// To satisfy Red Black Tree constraint #1, recolor root to black
r.Root.Color = BLACK
}
Re-run test to ensure red-black tree level constraint is satisfied:
go test -timeout 30s
# Output
ok github.com/srleyva/LSM/pkg/trees
Success: Tests passed.
Recap
In review, we've learned a tree data-structure that allows for self-balancing. It is important to realize that this balancing is relative and not perfect (sorry Thanos!). This tradeoff allows for faster insertions and deletions. AVL Trees, on the flip side, are more strictly balanced resulting in faster lookups and are more ideal for heavy read applications. However, the trade off here is insertion and removals are slower. This is why LSM Tree's tend to favor AVL trees over Red Black Trees. However, things like the Completely Fair Scheduler algorithm prefer faster deletions and insertions into the scheduler's timeline for future execution. In the next article, I will dive into deletions from a Red-Black Tree utilizing some of the functions we've already built. Until then, stay curious and stay healthy!



Top comments (1)
Right?! Just hope he doesn’t make half your data disappear 😂