
Ever looked at a credit card and wonder if the numbers on it means anything? Turns out those number are not entirely random, and instead follow a set of regular patterns. These patterns in turn allow merchants and others to not only validate the authenticity of the card, but also find other useful information about it. Here’s how they are generated.
Identifying the Card Issuer
The first six digits of the card, known as the Issuer Identification Number (INN) tell us about the who the issuer of the card is. Some example of this from the more well-known issuers are:
| Card Issuer | Card Number Range |
|---|---|
| Visa | 4xxxxx |
| MasterCard | 51xxxx-55xxxx, 222100-272099* |
| Discover | 6011xx, 644xxx, 65xxxx |
| American Express (Amex) | 34xxxx, 37xxxx |
or more strictly, the card numbers follow a set of regular expression patterns:
| Card Issuer | Card Number Range |
|---|---|
| Visa | ^4[0-9]{12}(?:[0-9]{3})?\$ |
| MasterCard | ^5[1-5][0-9]{14}\$ |
| Discover | see this page for full regex |
| American Express (Amex) | ^3[47][0-9]{13}\$ |
For those interested, a full list of all the RegEx each issuers can be found on this page
Note:
- As part of Mastercard’s 2-series expansion back in 2017, their cards can now begin with 2
Validating the Card Number
A typical string of credit card numbers can be divided into a couple of groups:
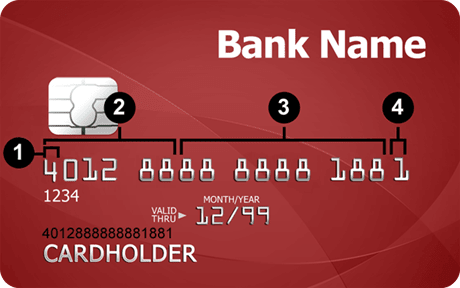
Based on the above diagram
- Major Industry Identifier (MII) - identifies the industry of the card. See here for the full list of industries and digit
- Issuer Identification Number (IIN) — identifies the issuer of the card. American Express starts with 34 or 37, Mastercard starts with 2221–2720 or 51–55, Visa starts with 4. See here for a list of all IIN ranges.
- Account Number — identifies the cardholder's account
- Checksum — makes sure that the account number is valid
Now we get to the cool bit. Luhn's Algorithm determines the validity of a card using the account number and checksum (labels 3 and 4).
- From the rightmost digit of your card number, double every digit
- If any digit is greater than 9 after the above doubling, add the digits of the result (i.e. 16 => 1+6 = 7). Alternatively, the same result can be achieved by subtracting 9 from the that result (i.e. 16 => 16-9 = 7)
- Sum up all of the digits
- If the sum ends in a zero, then the card is valid according to the Luhn formula
For example: Assume our card number is 4417 1234 5678 9113

Summing all of the digits in the last row together we get 70, which ends in a zero and thus our card is valid!
Algorithm Limitations
While Luhn's algorithm will detect any single-digit error, as well as almost all transpositions of adjacent digits, it cannot detect the transposition of the sequence "(first-valid-character)(last-valid-character)" to "(last-valid-character)(first-valid-character)" or vice versa. More specifically for our 0-9 digit set, it will not detect transposition of the two-digit pair '09' to '90' or vice versa. The reason and proof behind this weakness is quite mathematically involved but can be found here
Concluding
Now that we understand the general process of how to validate cards and identify who the issuer is, we can automate the process using a simple script. For those who are interested in how to write one, I be posting a short tutorial using Go in the coming weeks.


Top comments (0)