To understand what a binary search tree is, we should first go over the tree data structure.
Tree is a hierarchical or nonlinear data structure. It is a collection of elements, called nodes, that are linked to each other. Each node has two pieces of information: 1. the data value itself and 2. a pointer that references other nodes.
Each tree has a root node, which can have zero or more child nodes. The child nodes make the root node a parent node. Each of those child nodes could have their own child nodes and so on. It is therefore possible for a node to be both a child and a parent at the same time. Two child nodes that are next to each other are called siblings. Any node that does not have a child is a leaf.
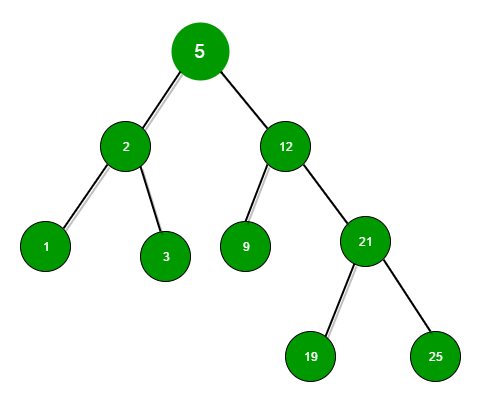
A binary tree is a type of tree where each node has a maximum of 2 children.
A binary search tree is a type of a binary tree that naturally stays sorted because it follows this rule:
- Every left child always be less than its parent
- Every right child always be greater than its parent
BST is balanced when its left and right subtrees have roughly the same amount of nodes. Otherwise it will be unbalanced.
If the left and right side of a BST have exactly the same number of nodes, then it is a perfect tree, which is actually quite rare.
class Node {
constructor(value) {
this.value = value
this.left = null
this.right = null
}
}
class BST {
constructor(value) {
this.root = new Node(value)
this.count = 1
}
size() {
return this.count
}
insert(value) {
this.count++
let newNode = new Node(value)
const searchTree = node => {
// if value < node.value, go left
if (value < node.value) {
// if no left child, append new node
if (!node.left) {
node.left = newNode
}
// if left child, look left again
else {
searchTree(node.left)
}
}
// if value > node.value, go right
else if (value > node.value) {
// if no right child, append new node
if (!node.right) {
node.right = newNode
}
// if right child, look right again
else {
searchTree(node.right)
}
}
}
searchTree(this.root)
}
}




Top comments (1)
What would you say are the applications of a binary search tree?