Binary search
Suppose you’re searching for a person in the phone book (what an old-
fashioned sentence!). Their name starts with K. You could start at the
beginning and keep flipping pages until you get to the *K*s. But you’re
more likely to start at a page in the middle, because you know the *K*s
are going to be near the middle of the phone book.
Or suppose you’re searching for a word in a dictionary, and it
starts with O. Again, you’ll start near the middle.
Now suppose you log on to Facebook. When you do, Facebook
has to verify that you have an account on the site. So, it needs to
search for your username in its database. Suppose your username is
KingJulien. Facebook could start from the *A*s and search for your
name—but it makes more sense for it to begin somewhere in the
middle.
This is a search problem. And all these cases use the same algorithm
to solve the problem: binary search.
Binary search is an algorithm; its input is a sorted list of elements
(I’ll explain later why it needs to be sorted). If an element you’re
looking for is in that list, binary search returns the position
where it’s located. Otherwise, binary search returns null.
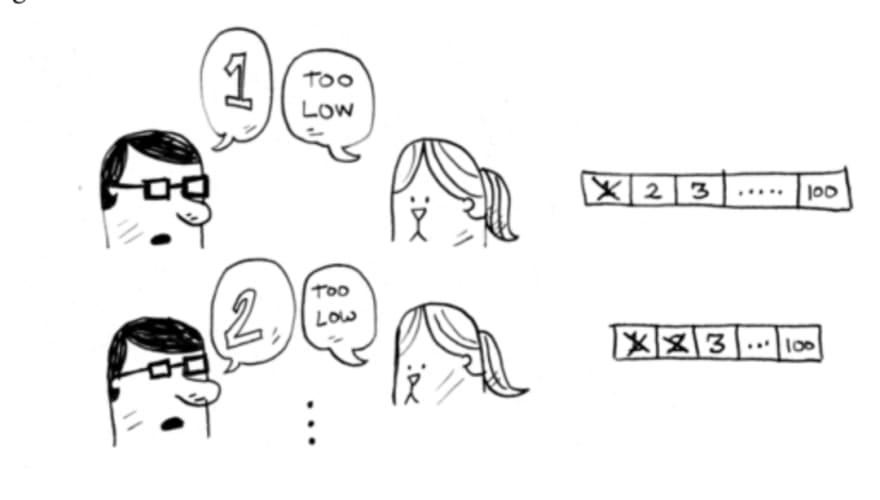
Here’s an example of how binary search works. I’m thinking of a
number between 1 and 100.
You have to try to guess my number in the fewest tries possible. With
every guess, I’ll tell you if your guess is too low, too high, or correct.
Suppose you start guessing like this: 1, 2, 3, 4 .... Here’s how it would
go.
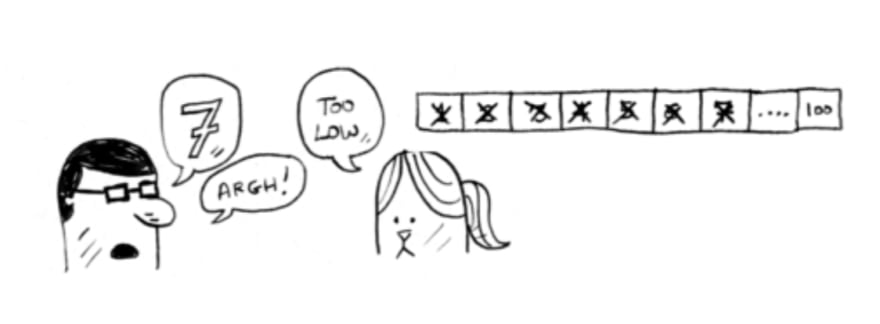
This is simple search (maybe stupid search would be a better term). With each guess, you’re eliminating only one number. If my number was 99,
it could take you 99 guesses to get there!
A better way to search
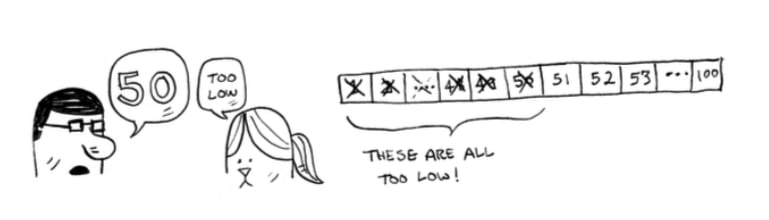
Here’s a better technique. Start with 50.
Too low, but you just eliminated half the numbers! Now you know that 1–50 are all too low. Next guess: 75.
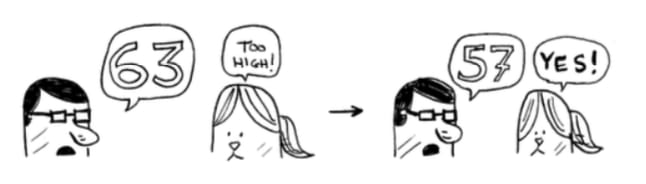
Too high, but again you cut down half the remaining numbers! With binary search, you guess the middle number and eliminate half the remaining numbers every time. Next is 63 (halfway between 50 and 75).
This is binary search. You just learned your first algorithm! Here’s how many numbers you can eliminate every time.
Whatever number I’m thinking of, you can guess in a maximum of seven guesses—because you eliminate so many numbers with every guess!
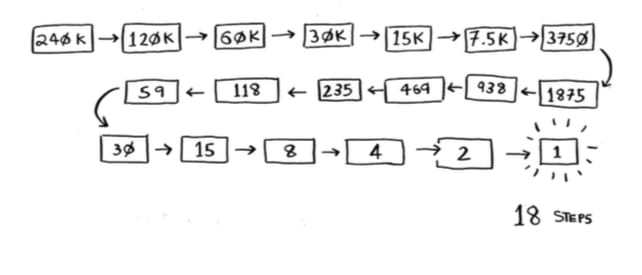
Suppose you’re looking for a word in the dictionary. The dictionary has 240,000 words. In the worst case, how many steps do you think each search will take?
Simple search could take 240,000 steps if the word you’re looking for is the very last one in the book. With each step of binary search, you cut the number of words in half until you’re left with only one word.
So binary search will take 18 steps—a big difference! In general, for any list of n, binary search will take log2 n steps to run in the worst case, whereas simple search will take n steps.
function binarySearch (array, target) {
// Define Start and End Index
let startIndex = 0;
let endIndex = array.length - 1; // While Start Index is less than or equal to End Index
while(startIndex <= endIndex) { // Define Middle Index (This will change when comparing )
let middleIndex = Math.floor((startIndex + endIndex) / 2); // Compare Middle Index with Target for match
if(target === array[middleIndex]) {
return console.log("Target was found at index " + middleIndex);
} // Search Right Side Of Array
if(target > array[middleIndex]) {
console.log("Searching the right side of Array")
// Assign Start Index and increase the Index by 1 to narrow search
startIndex = middleIndex + 1;
} // Search Left Side Of Array
if(target < array[middleIndex]) {
// Assign End Index and increase the Index by 1 to narrow search
console.log("Searching the left side of array")
endIndex = middleIndex - 1;
} // Not found in this iteration of the loop. Looping again.
else {
console.log("Not Found this loop iteration. Looping another iteration.")
}
} // If Target Is Not Found
console.log("Target value not found in array");
}






Top comments (0)