## Introduction
Tree data structures are built using tree nodes (a variation on the nodes you created earlier) and are another way of storing information. Specifically, trees are used for data that has a hierarchical structure, such as a family tree or a computer’s file system. The tree data structure you are going to create is an excellent foundation for further variations on trees, including AVL trees, red-black trees, and binary trees - which you will actually create in a lesson later on!
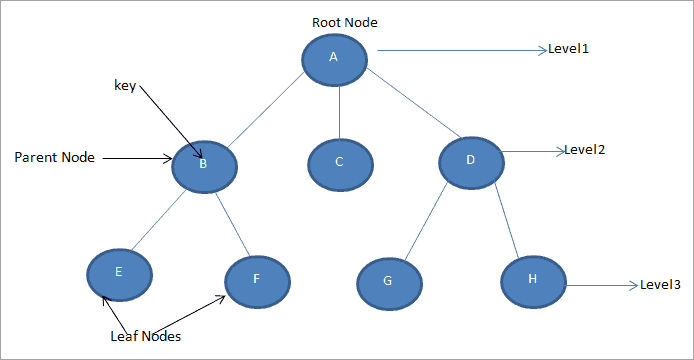
Tree Detail
Trees grow downwards in computer science, and a root node is at the very top. The root of this tree is /photos.
/photos references to two other nodes: /safari and /wedding. /safari and /wedding are children or child nodes of /photos.
Conversely, /photos is a parent node because it has child nodes.
/safari and /wedding share the same parent node, which makes them siblings.
Note that the /safari node is child (to /photos) and parent (to lion.jpg and giraffe.jpg). It’s extremely common to have nodes act as both parent and child to different nodes within a tree.
When a node has no children, we refer to it as a leaf node.
Image credits to softwaretestinghelp
Tree Varietals
Trees come in various shapes and sizes depending on the dataset modeled.
Some are wide, with parent nodes referencing many child nodes.
Some are deep, with many parent-child relationships.
Trees can be both wide and deep, but each node will only ever have at most one parent; otherwise, they wouldn’t be trees!
Each time we move from a parent to a child, we’re moving down a level. Depending on the orientation we refer to this as the depth (counting levels down from the root node) or height (counting levels up from a leaf node).
Binary Search Tree
Constraints are placed on the data or node arrangement of a tree to solve difficult problems like efficient search.
A binary tree is a type of tree where each parent can have no more than two children, known as the left child and right child.
Further constraints make a binary search tree:
Left child values must be lesser than their parent.
Right child values must be greater than their parent.
The constraints of a binary search tree allow us to search the tree efficiently. At each node, we can discard half of the remaining possible values!
Let’s walk through locating the value 31.
Start at the root: 39
31 < 39, we move to the left child: 23
23 < 31, we move to the right child: 35
31 < 35, we move to the left child: 31
We found the value 31!
In a dataset of fifteen elements, we only made three comparisons. What a deal!
Image credits to Breaking Down Breadth-First Search
Post from Medium
Tree Review
Trees are useful for modeling data that has a hierarchical relationship which moves in the direction from parent to child. No child node will have more than one parent.
To recap some terms:
- root: A node which has no parent. One per tree.
- parent: A node which references other nodes.
- child: Nodes referenced by other nodes.
- sibling: Nodes which have the same parent.
- leaf: Nodes which have no children.
- level: The height or depth of the tree. Root nodes are at level 1, their children - are at level 2, and so on.



Top comments (0)