In the previous examples, we calculated Poisson probability on a single data point. Here, I am going to calculate the probabilities of soccer teams scoring a particular number of goals in a match. These probabilities are used to get odds based on historical results. I would like to note that it is a simplified approach because it does not account for the other important factors and features, e.g. injured players, players’ position for the particular match, new players and coaches, etc. I used the English Premier League data for this analysis, the link to the data source is here.
Game outcome probabilities
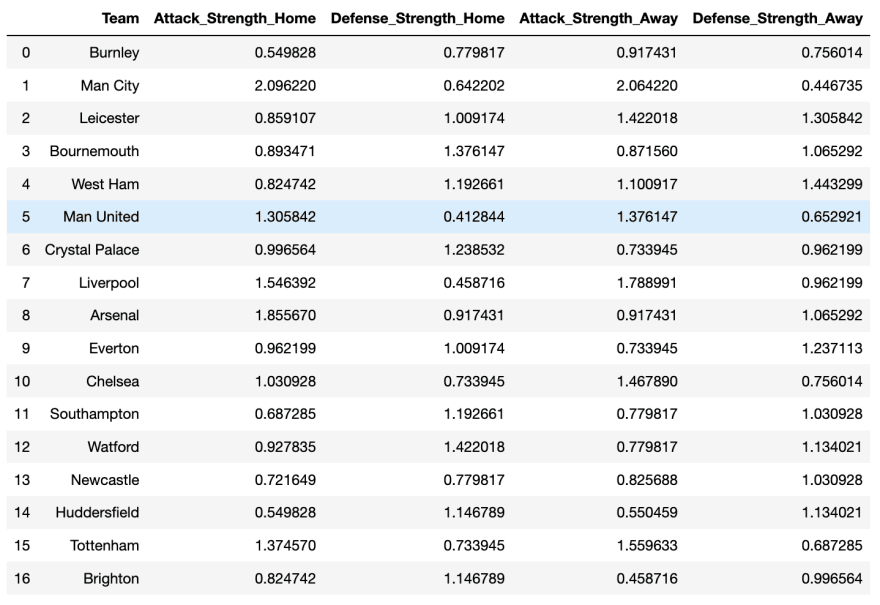
I used season 2017-2018 data to calculate teams’ defense and attack strength. 20 teams played 380 games total. Because there were 3 new teams in the season 2018-19, I showed only 17 teams' results. You can find a Python script here.
Let’s apply 2017-18 historical data to calculate the outcome probabilities of the first matches in season 2018-19. Particularly, we convert probabilities of scoring n number of goals to the home team win, away team win, and draw.
Conclusion
In this example out of 14 games, the results of 11 games correlated with calculated probabilities. As I have already mentioned in the beginning, these probabilities do not account for the specifics of the particular games. Also, here I skipped a test which checks whether a Poisson distribution is a good approximation.
As part of feature engineering, I would like to check if the above approach could be adjusted for the horse races, e.g. using gate numbers instead of home and away teams.




Top comments (0)