In this weeks article I'll be discussing heaps. We'll go over how to implement a heap in javascript, but first let's go over what a heap is.
What is a heap?
A heap is an almost complete tree like data structure that satisfies the heaps property.
Let's dissect this definition. First, we need to know what a complete tree is. A complete tree is a tree data structure where every node is filled except for the last level.
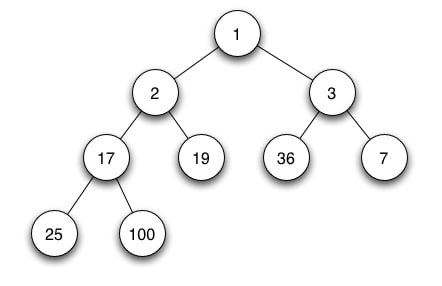
Next we need to know what properties a heap can have. Heaps are often structures in one of two ways. As a min heap, or as a max heap. A min heap is a heap where the parent node is greater than it's children. A max heap is a heap where the parent node is less than it's children. Furthermore, heaps can be classified as a binary heap if each node only has two children. Below is an example of a non-complete binary min heap.
Why use a heap?
The main use for a heap is a priority queue. A priority queue is a normal queue where each element has an additional value that indicates the priority it should exit the queue. Heaps are a perfect fit for priority queues because they support insert, delete, and extract max/min methods in O(logn) time.
Implementation of a heap
Now that we've got through all of that let's learn how to go about implementing a heap. Due to heaps being a tree like structure you would think that implementing one would be similar to implementing a tree. However, due to the ordered structure of a heap we actually are going to be storing our heap in an array.
We are able to store our heap in an array compactly because we don't need to use any pointers. We are instead able to locate the parent and children through arithmetic using the indicies of the array.
Let's start with the heap class. All we need to do is create an empty array. For this implementation we'll be making a minHeap.
From here we'll need a few helper methods that we'll use for our main functionality. First we'll need a method to swap the location of two elements in our heap given their indexes. This can cleanly be done in one line using ES6 syntax, nice!
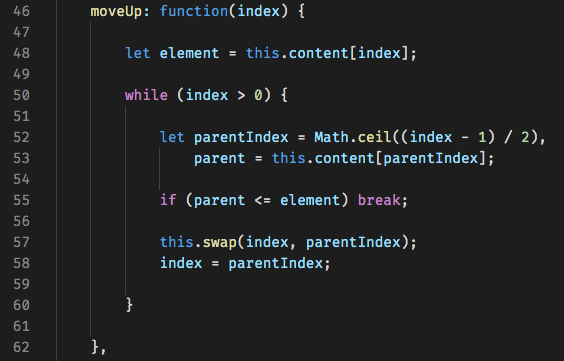
Next we'll need a method that takes an element and moves it up the tree until it is placed into the right location. We'll pass the method the index of the element we want to move. We'll then continuously loop, each time comparing current element with its parent. If the parent is greater than the current element, we'll swap their locations and repeat the process until the element is in the correct location.
Notice how we are able to locate the parent note with a basic equation.
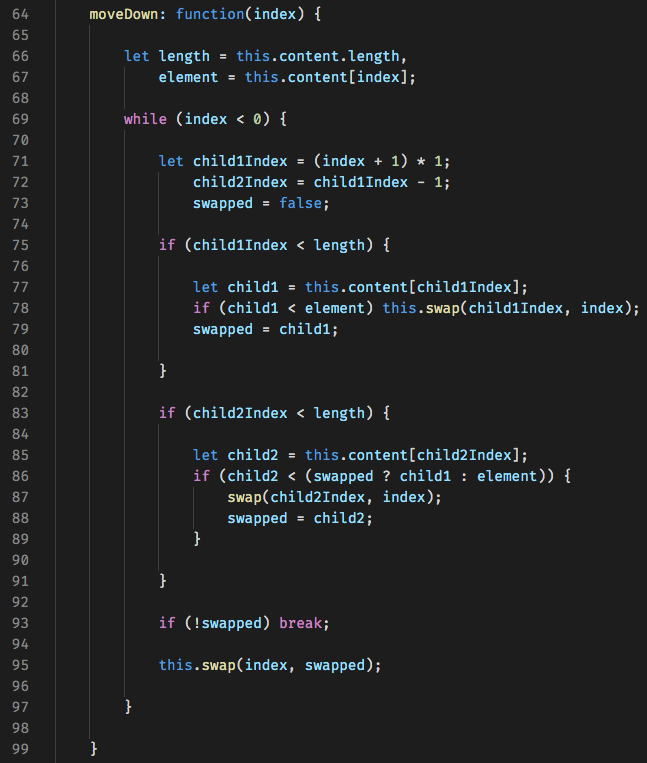
Similar to the moveUp method, we'll need a method to move an element down the tree. This method will be of a similar structure except we'll be comparing the parent to both of its children.
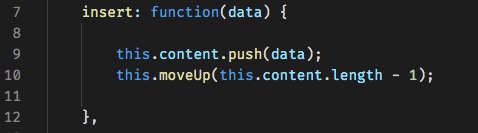
Now that we have our helper methods we can easily implement the main functions of our heap. First, we need a method to insert elements into our heap. All we need to do is push our element to the end of our heap then move it up.
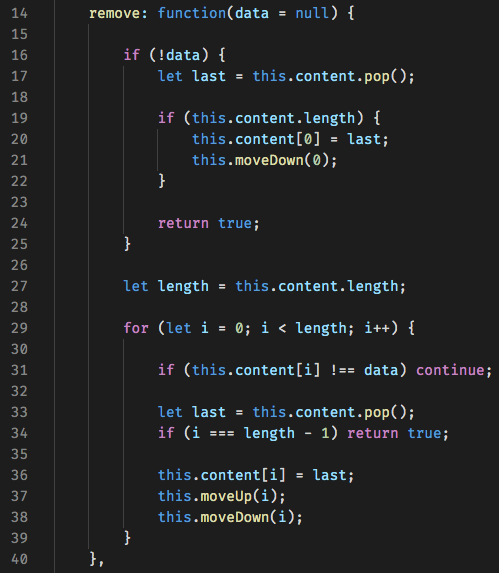
Next, we need a method to remove elements from the heap. This method is going to be a two in one. It defaults the argument to null so that when nothing is passed in we remove the last element from the heap. Otherwise, the method removes the specified node.
Thanks for reading! As usual, the code from this post can be found here.

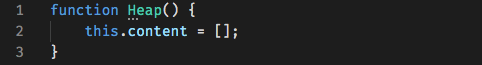


Top comments (0)