In the previous post, we discussed what a loss function is for a neural network and how it helps us to train the network in order to produce better, more accurate results. In this post, we will see how we can use gradient descent to optimize the loss function of a neural network.
Gradient Descent
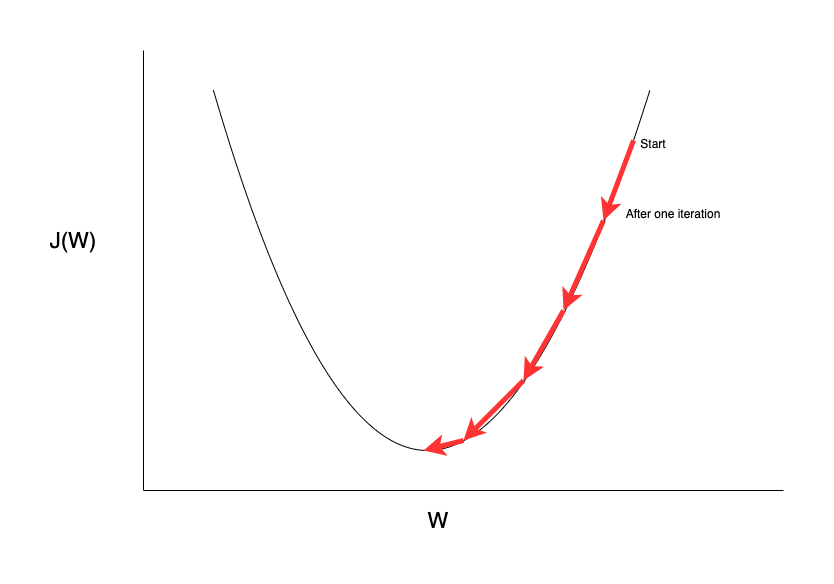
Gradient Descent is an iterative algorithm to find the minimum of a differentiable function. It uses the slope of a function to find the direction of descent and then takes a small step towards the descent direction in each iteration. This process continues until it reaches the minimum value of the function.
Let's say we want to optimize a function J(W) with respect to the parameter W. We can summarize the working of the Gradient Descent algorithm as follows:
- Start at any random point on the function.
- Calculate the slope of the function at that point.
- Take a small step in the direction opposite to the slope of the function.
- Repeat until it reaches the minimum value.
The algorithm works in the same way for any N-dimensional differentiable function. The example above shows a 2D plot because it is easier for us to visualize.
For our neural network, we need to optimize the value of our loss function J(W), with respect to the weights(W) in the used in the network. We can write the algorithm as:
Algorithm
Learning Rate
The parameter 
- A small learning rate means that the algorithm will take small steps in each iteration and will take a long time to converge.
- A very large learning rate can cause the algorithm to overshoot the point of minimum value and then overshoot again in the opposite direction, which can eventually cause it to diverge.
To find an optimum learning rate, it is a good idea to start with something small, and slowly increase the learning rate if it takes a long time to converge.
Conclusion
To summarize the basics of a neural network:
- Perceptron is the basic building block of a neural network. It multiplies an input with a weight and applies a non-linearity to the product.
- Perceptrons connect together to form a layer of a neural network. There are multiple set of weights between different layers.
- To train the network we choose a loss function and then optimize the loss functions with respect to the weights W using gradient descent.
This concludes this series on the basics of neural networks. I would love to hear your views and feedback. Feel free to hit me up on Twitter.




Top comments (0)