Introduction
Suppose you are looking for a particular value of a characteristic of a population, firstly data is obtained from a sample of that population(could be the mean), and the parameter is guessed from the sampled data. Due to not using the whole population, one may ask if the sampled data is a reliable estimation of the whole population. This is where confidence interval comes in.
Confidence Interval
As earlier mentioned, the range of values that you expect your estimate to lie within, within a certain level of confidence is the confidence interval. For instance, if you say you have a 90% confidence level, it means you are very confident that 90% of the time, your estimate falls between the lower and upper bounds which are specified by that confidence interval.
There's a value called the alpha value, which indicates a threshold, for instance, an alpha of 0.1, which means that there's a less than 10% chance that the test could have occurred under the null hypothesis. Coming back to our confidence level, the desired confidence level is normally 1 minus this alpha value used in the statistical testing.
Therefore, if an alpha value of p < 0.1 is chosen for statistical significance, then the confidence level would ultimately be 1-0.1= 0.9 or 90%.
Confidence intervals are used for various statistical estimates such as
- Proportions
- Mean of a population
- Differences that exist between the mean and proportions of a population
- the variation estimates among groups
As the same suggests, these are all estimates of a number and do not give valuable information around that number, but the confidence interval is a good way to know more information about the variations of the number.
You can find more in the following article Confidence Interval Understanding


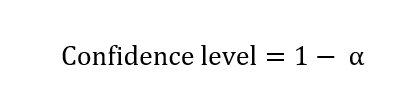

Top comments (0)