Definition
Binary Search is a searching algorithm used in a sorted array by repeatedly dividing the search interval in half. The idea of binary search is to use the information that the array is sorted and reduce the time complexity to O(Log n).
Comparsion
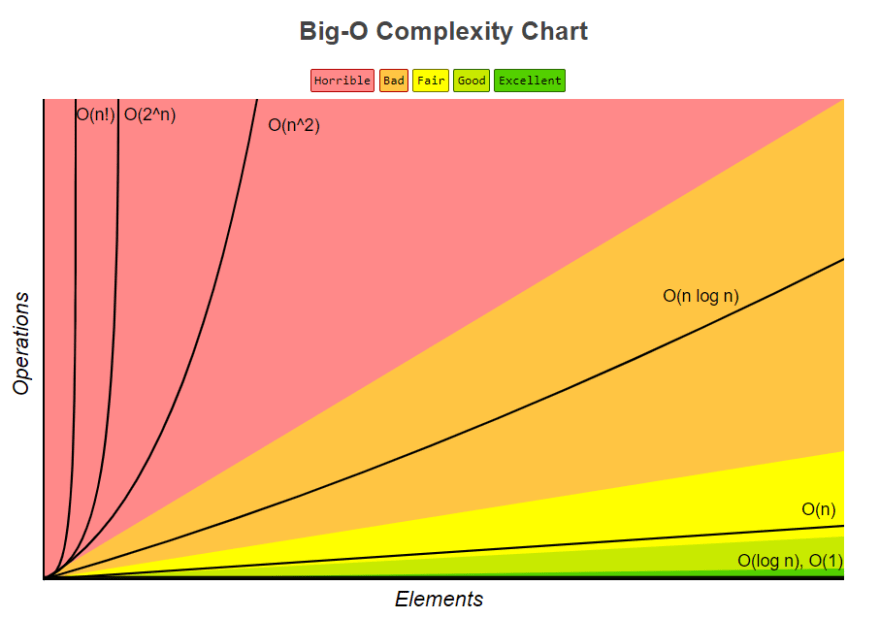
Binary Search Big O Notation is O(log n), Compared to Linear Search which Has Time Complexity of O(n).
Binary Search is able to search sorted arrays much faster than Linear Search.
Real Life Example
I'm thinking of a number from 1 to 50, The answer is 1
Linear Search
Number = 50 ? No
Number = 49 ? No
...
Number = 2 ? No
Number = 1 ? Yes!
It takes 50 Guesses at Worst Case!
Binary Search
Number = 25 ? No, Less
Number = 12 ? No, Less
Number = 6 ? No, Less
Number = 3 ? No, Less
Number = 2 ? No, Less
Number = 1 ? Yes!
It takes 6 Guesses at Worst Case!
Conclusion
Assuming 1,000,000 Numbers!
Linear Search would result in a 1,000,000 Guesses (Worst Case)
Binary Search would result in a 20 Guesses (Worst Case)
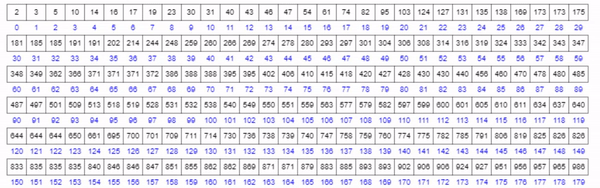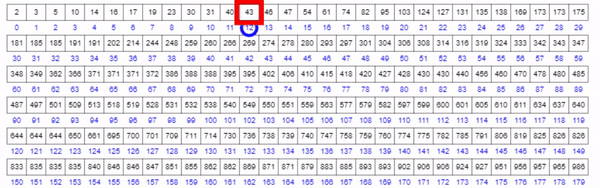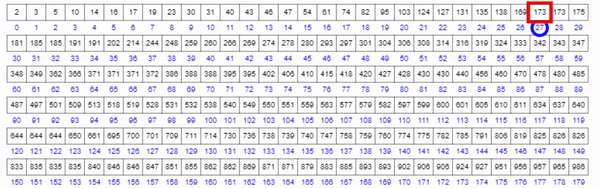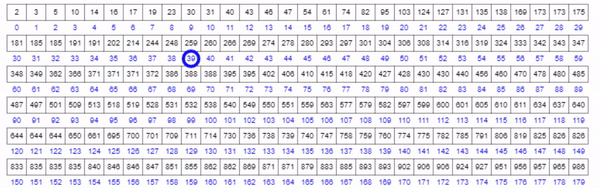
Visualization
Binary Search
Linear Search
Coding
const binarySearch = (sortedArr, value) => {
let left = 0;
let right = sortedArr.length - 1;
while (left <= right) {
const mid = Math.floor((left + right) / 2);
const midVal = sortedArr[mid];
if (midVal === value) {
return mid;
} else if (midVal < value) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
};




Top comments (1)