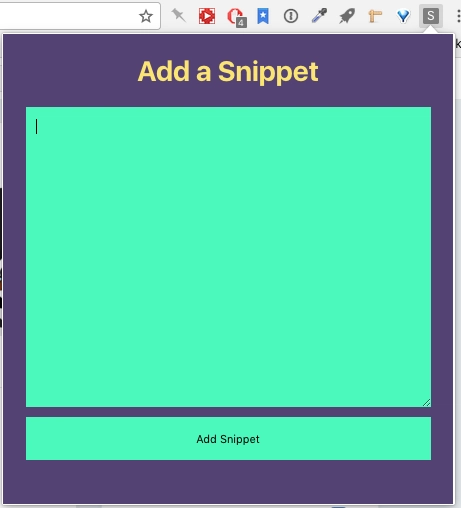
Welcome back to a second tutorial on the basics of chrome extensions. If you haven't read the first tutorial you can read it here. In part one we explored how an extension can be used to modify the websites we visit, where as now we are going to create a very basic web component (it can't be called a full website) that "pops up" when the extension icon is clicked. Here's a screenshot of the end product.
This is going to be a basic version of extensions like evernote's web clipper. By the end, we will be able to highlight some code and have it apear in the textbox above.
Setup
As covered in the first tutorial, everything we intend to do, we need to specify in the manifest.json file:
{
"manifest_version": 2,
"name": "Snip Da",
"version": "0.1",
"browser_action": {
"default_icon": "icon.png",
"default_popup": "popup.html"
}
}
browser_action is the new property we didn't need to use in the first tutorial. From the documentation browser_action is described as:
Use browser actions to put icons in the main Google Chrome toolbar, to the right of the address bar. In addition to its icon, a browser action can also have a tooltip, a badge, and a popup.
As you can see, we added a popup. That's the html file where we'll create the component.
In the extension root directory we need to have an icon.png file and a popup.html. Further more, we will need to have a stylesheet and a JavaScript file with the same name as the HTML file: popup.js and popup.css. Using the same name for the extra resource files enables their use in the popup.html.
Now let's write the HTML code in popup.html:
!doctype html>
<html>
<head>
<title>Add a Snippet</title>
<script src="popup.js"></script>
<link rel="stylesheet" type="text/css" href="popup.css">
</head>
<body>
<h1>Add a Snippet</h1>
<form id="form">
<textarea id="code"></textarea>
<button type="submit" id="checkPage">Add Snippet</button>
</form>
</body>
</html>
Once again, we are able to link to popup.js and popup.css because they have the same name as the HTML file.
The entire CSS code is not very important, you can style this in any way you want or clone the repo, however the following snippet is worth noting:
body{
width: 450px;
height:450px;
}
The width and height effect the actual window.
As for the JavaScript code, in popup.js it can be general JavaScript. Logically we would like something to happen when the form is submitted
document.addEventListener('DOMContentLoaded', function() {
let form = document.getElementById('form');
form.addEventListener('submit', function(e){
e.preventDefault();
let value = e.target.children.code.value
console.log(code)
})
}, false);
The code has to be wrapped with an event listener of DOMContentLoaded, the MDN web docs describes this event as:
The DOMContentLoaded event is fired when the initial HTML document has been completely loaded and parsed, without waiting for stylesheets, images, and subframes to finish loading.
Then of course, if this was a real extension, on submit we'd push the code snippet to some API.
Tip: the console of the extension can be accessed on right-click then selecting inspect
Access between windows
What we really want to do is be able to highlight some text in the browser and have it automatically show up in our extension form. Exactly like this:
To accomplish this we need to take content from the main browser window. This is similar to what we already done in the first tutorial. Hence we need to specify our intention in the manifest.json:
{
// ...
"content_scripts": [
{
"matches": [
"<all_urls>"
],
"js": ["content.js"]
}
]
}
With that configuration, we create a content.js file and here we have access to the main browser window. If we visit dev.to, with content.js we are able to modify the rendered HTML after it's loaded. Let's use the following code:
document.onmouseup = document.onkeyup = document.onselectionchange = function() {
let content = window.getSelection().toString();
};
With that, we are one step further, content has the content which we selected. Now we need to access the content in our extension.
Consider the extension window and the current tab as two different tabs. They have no connection with each other. So the best way to transfer content from one tab to the other is through local storage.
With that, the above code needs a new line:
document.onmouseup = document.onkeyup = document.onselectionchange = function() {
let content = window.getSelection().toString();
chrome.storage.sync.set({ content });
};
The usage of chrome.storage is recommended by chrome documentation:
Use the chrome.storage API to store, retrieve, and track changes to user data.
And finally, let's get the content from the storage and into our extension's form:
let code = document.getElementById('code');
chrome.storage.sync.get(stored => {
code.value = stored.content
})
(code is the ID of the textarea)
So when we open the extension, the textarea would have the content we selected.
Declare Permissions
So far we used the manifest.json file to make our own file available, but we also need to declare the parts of chrome's APIs we want to be using. From the documentation we learn that much:
To use most chrome.* APIs, your extension or app must declare its intent in the "permissions" field of the manifest.
There are two APIs we are using, the storage, obviously, and activeTab which is not so obvious.
As it's clear by now, we intend to go on any tab, select some text and have it appear in our extension form. Right now it would not work because we don't have permission to use chrome's local storage. However, without also gaining permission for activeTab, our extension would not listen to all active tabs. The official description of activeTab being:
The activeTab permission gives an extension temporary access to the currently active tab when the user invokes the extension - for example by clicking its browser action. Access to the tab lasts until the tab is navigated or closed.
So, lastly, let's specify our intend to use these two APIs. In manifest.json file, add:
...
"permissions": [
"storage",
"activeTab"
]
Conclusion
There you have it. Between the previous tutorial and this, we have covered the basics of how to develop an extension. The code for this tutorial can be found in the folder named extensionTwo_snipDa on the same repository as the previous one.
There is at least one more thing that can be done with chrome extensions, and that is providing options to the user. I might write a tutorial on that soon, but for now I'm really happy with the results.
Thanks for reading



Top comments (5)
Hi, nice post! :D
Have you ever tried to make a toolbar-like extension?
I wanted to do that, but seems impossible to make it work on every page...
Here is a basic recipe, but when you
translateY()thebodydown, some pages get broken, like Facebook or Stackoverflow.I guess I'll have to override new tab page (but there are already plugins like that).
Any suggestions?
The bookmarks toolbar is a toolbar, if that's what you mean, I have no idea ( don't know if that's possible to do). But in the link StumbleUpon is mentioned. They do this:
It looks like the are using the approach I explored in part one. I had StumbleUpon installed for a while and whilst I never looked into it, it looks definitely as though they used that approach rather than this one
Now you got me hooked, please let me know if I understood you and if the first approach is the kind of thing you are looking for (all though the tutorial is very basic)
edit - From a quick google search other developers that make tutorials on "how to create a toolbar" are simply adding a navigation bar on the page, so, yes if that's what you want, this is not what you need, the first tutorial is for you.
Well, I basically wanted to REPLACE original bookmarks toolbar, like this:

Only way to do that is to use a content script (like in your first tutorial). To add my
divto thebodyand position it. That's all I want.. :DCool
Hi Aurel, great posts! Loved them <3!
For the part where we have to get the highlighted text from a webpage, I have done it without local storage by using chrome.tabs.executeScript
Would this cause any issue? I'm a new developer wrt chrome extensions. Any help would be great! :)
Thanks.