Segmentation and Feature Extraction
(You can view the version with all the audio segments here
In part 1 we learned some basic signal processing terminology, as well as how to load and visualize a song. In this post we will discuss how to break up a signal (segment) and extract various features from it. Then, we'll do some exploratory analysis on the features so that we can get an idea of the interactions among features.
Why do we want to segment a song?
Songs vary a lot over time. By breaking up this heterogenous signal in to small segments that are more homogenous, we can keep the information about how a song changes. For example, say that we have some features such as 'danceability'. Imagine a song that is at first very quiet and low energy, but as the song progresses, it becomes a full blown Rihanna club anthem. If we just examined the average danceability of the entire song, it might be lower than how danceable the song actually is. This context and distinction is important because if we are running a classifier or clustering algorithm on each segment of a song, we could classify that song as the club anthem that it is, not just it's (below) average.
Segment a song using onset detection
An onset in a signal is often described as the beginning of a note or other sound. This is usually found by measuring peaks in energy along a signal. If we find that peak in energy, and then backtrack to a local minimum, we have found an onset, and can use that as a boundary for a segment of a song.
here are some good resources for learning more about onsets and onset detection: https://musicinformationretrieval.com/onset_detection.html, https://en.wikipedia.org/wiki/Onset_(audio), https://www.music-ir.org/mirex/wiki/2018:Audio_Onset_Detection
%matplotlib inline
import librosa
import numpy as np
import IPython.display as ipd
import sklearn
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
plt.rcParams['figure.figsize'] = (16, 7)
By default, onset_detect returns an array of frame indices that correspond to frames in a signal. We actually
want the sample indices so that we can slice and dice our signal neatly with those indices. We'll continue to use our Rock & Roll example from the previous post.
signal, sr = librosa.load('/Users/benjamindykstra/Music/iTunes/Led Zeppelin/Led Zeppelin IV/02 Rock & Roll.m4a')
# use backtrack=True to go back to local minimum
onset_samples = librosa.onset.onset_detect(signal, sr=sr, backtrack=True, units='samples')
print onset_samples.shape
(132,)
We have found 132 segments in the song. Now, lets use the sample indices to split up the song in to subarrays like so:
[[segment 1], [segment 2], ..... [segment n]]. Each segment will be a different length, but when we calculate a feature vector for a segment, the feature vector will be a standard size. The final dimensions of the data after segmenting and calculating features for each segment will be (# segments, # features).
# return np array of audio segments, within each segment is the actual audio data
prev_ndx = 0
segmented = []
for sample_ndx in onset_samples:
# get the samples from prev_ndx to sample_ndx
segmented.append(np.array(signal[prev_ndx:sample_ndx]))
prev_ndx = sample_ndx
segmented.append(np.array(signal[onset_samples[-1]:])) # gets the last segment from the signal
segmented = np.array(segmented)
segmented.shape
(133,)
As a sanity check, if we concatenate all the segments together, it should be equal in shape to the original signal.
print "difference in shapes: {}".format(signal.shape[0] - np.concatenate(segmented).shape[0])
difference in shapes: 0
Listen to a few segments together!
ipd.Audio(np.concatenate(segmented[25:30]), rate=sr)
or just a single short segment
ipd.Audio(segmented[21], rate=sr)
Lets define a more generic segmentation function for use later on
def segment_onset(signal, sr=22050, hop_length=512, backtrack=True):
"""
Segment a signal using onset detection
Parameters:
signal: numpy array of a timeseries of an audio file
sr: int, sampling rate, default 22050 samples per a second
hop_length: int, number of samples between successive frames
backtrack: bool, If True, detected onset events are backtracked to the nearest preceding minimum of energy
returns:
dictionary with attributes segemented and shape
"""
# Compute the sample indices for estimated onsets in a signal
onset_samples = librosa.onset.onset_detect(signal, sr=sr, hop_length=hop_length, backtrack=backtrack, units='samples')
# return np array of audio segments, within each segment is the actual audio data
prev_ndx = 0
segmented = []
for sample_ndx in onset_samples:
segmented.append(np.array(signal[prev_ndx:sample_ndx]))
prev_ndx = sample_ndx
segmented.append(np.array(signal[onset_samples[-1]:]))
return { 'data': np.array(segmented), 'shape': np.array(segmented).shape }
Feature Extraction
Now that we have a way to break up a song, we would like to be able to derive some features from the raw signal. Librosa has a plethora of features to choose from. They fall in to two categories, spectral and rhythmic features. Spectral features are features that have to do with the frequency, pitch and timbre of a signal, where as rhythmic features (you guessed it) give you info about the rhythm of the signal.
The objective with feature extraction is to feed a single function a single segment of a song, that returns an array of the calculated features for that segment
Some of the feature methods return arrays of differing shapes and we need to account for those differences in our implementation. For example, when calculating the Mel-frequency cepstral coefficients for a segment, the return shape is (# of coefficients, # of frames in a segment). Since we're assuming that a segment is a homogenous piece of signal, we should take the average of the coefficients across all the frames so we get a shape of (# of coefficients, 1).
First I will define all the feature functions, and then I will explain what information they add/describe.
def get_feature_vector(segment):
'''
Extract features for a given segment
Parameters:
segment: numpy array, a time series of audio data
Returns:
numpy array
'''
if len(segment) != 0:
feature_tuple = (avg_energy(segment), avg_mfcc(segment), zero_crossing_rate(segment), avg_spectral_centroid(segment), avg_spectral_contrast(segment), bpm(segment))
all_features = np.concatenate([feat if type(feat) is np.ndarray else np.array([feat]) for feat in feature_tuple])
n_features = len(all_features)
return all_features
return np.zeros((30,)) # length of feature tuple
def avg_energy(segment):
'''
Get the average energy of a segment.
Parameters:
segment: numpy array, a time series of audio data
Returns:
float, the mean energy of the segment
'''
if len(segment) != 0:
energy = librosa.feature.rmse(y=segment)[0]
# returns (1,t) array, get first element
return np.array([np.mean(energy)])
def avg_mfcc(segment, sr=22050, n_mfcc=20):
'''
Get the average Mel-frequency cepstral coefficients for a segment
The very first MFCC, the 0th coefficient, does not convey information relevant to the overall shape of the spectrum.
It only conveys a constant offset, i.e. adding a constant value to the entire spectrum. We discard it.
BE SURE TO NORMALIZE
Parameters:
segment: numpy array, a time series of audio data
sr: int, sampling rate, default 22050
n_mfcc: int, the number of cepstral coefficients to return, default 20.
Returns:
numpy array of shape (n_mfcc - 1,)
'''
if (len(segment) != 0):
components = librosa.feature.mfcc(y=segment,sr=sr, n_mfcc=n_mfcc ) # return shape (n_mfcc, # frames)
return np.mean(components[1:], axis=1)
def zero_crossing_rate(segment):
'''
Get average zero crossing rate for a segment. Add a small constant to the signal to negate small amount of noise near silent
periods.
Parameters:
segment: numpy array, a time series of audio data
Returns:
float, average zero crossing rate for the given segment
'''
rate_vector = librosa.feature.zero_crossing_rate(segment+ 0.0001)[0] # returns array with shape (1,x)
return np.array([np.mean(rate_vector)])
def avg_spectral_centroid(segment, sr=22050):
'''
Indicate at which frequency the energy is centered on. Like a weighted mean, weighting avg frequency by the energy.
Add small constant to audio signal to discard noise from silence
Parameters:
segment: numpy array, a time series of audio data
sr: int, sampling rate
Returns:
float, the average frequency which the energy is centered on.
'''
centroid = librosa.feature.spectral_centroid(segment+0.01, sr=sr)[0]
return np.array([np.mean(centroid)])
def avg_spectral_contrast(segment, sr=22050, n_bands=6):
'''
considers the spectral peak, the spectral valley, and their difference in each frequency subband
columns correspond to a spectral band
average contrast : np.ndarray [shape=(n_bands + 1)]
each row of spectral contrast values corresponds to a given
octave-based frequency, take average across bands
Parameters:
segment: numpy array, a time series of audio data
sr: int, sampling rate
n_bands: the number of spectral bands to calculate the contrast across.
Returns:
numpy array shape (n_bands,)
'''
contr = librosa.feature.spectral_contrast(segment, sr=sr, n_bands=n_bands)
return np.mean(contr, axis=1) # take average across bands
def bpm(segment, sr=22050):
'''
Get the beats per a minute of a song
Parameters:
segment: numpy array, a time series of audio data,
sr: int, sampling rate
Returns:
int, beats per minute
'''
tempo = librosa.beat.tempo(segment) #returns 1d array [bpm]
return np.array([tempo[0]])
Selected Feature Justification
Energy:
The energy for a segment is important because it gives a feel for tempo and/or mood of a segment. It's actually just the root mean square of a signal.
MFCC:
The Mel-frequency cepstral coefficients relay information about the timbre of a song. Timbre describes the 'quality' of a sound. If you think about how an A note on a trumpet sounds vastly different than that same A on a piano, those differences are due to timbre.
Zero Crossing Rate:
Literally the rate at which a signal crosses the horizontal axis. It often corresponds to events in the signal such as a snare drum or some other percussive event.
Spectral Centroid:
I think the spectral centroid is actually really cool. It's a weighted average of the magnitude of the frequencies in a signal and a 'center of mass'. It's often perceived as a measure of the brightness of a sound.
Spectral Contrast:
An octave based feature, it more directly represents the spectral characteristics of a segment. Coupled with MFCC features, they can provide a lot of information about a signal.
Beats Per Minute:
Provides information about the tempo and (some) percussive elements of a song.
Now what do we actually do with all these features??? We can use them to cluster!!
def extract_features(all_songs):
'''
all_songs is a list of dictionaries. Each dictionary contains the attributes song_name and data.
The data are the segments of the song.
'''
all_song_features = []
song_num = 0
for song in all_songs:
print "Processing {} with {} segments".format(song['song_name'], len(song['data']))
song_name = song['song_name']
segment_features = []
for segment in song['data']:
feature_vector = get_feature_vector(segment)
segment_features.append(feature_vector)
song_feature_vector = np.array(segment_features)
print "shape of feature vector for entire song: {}".format(song_feature_vector.shape)
print "shape of segment feature vector: {}".format(song_feature_vector[0].shape)
n_seg = song_feature_vector.shape[0]
feature_length = song_feature_vector[0].shape[0]
song_feature_vector = np.reshape(song_feature_vector, (n_seg, feature_length))
all_song_features.append(song_feature_vector)
song_num += 1
all_feature_vector = np.vstack(all_song_features)
return all_feature_vector
Visualizing the features of two very different songs
Lets look at the features of Rock 'n Roll by Led Zeppelin, and I Remember by Deadmau5.
rock_n_roll = segment_onset(signal)
rock_n_roll['data'].shape
(133,)
feature_vec_rock = extract_features([{'song_name': '02 Rock & Roll.m4a', 'data': rock_n_roll['data']}])
feature_vec_rock.shape
Processing 02 Rock & Roll.m4a with 133 segments
shape of feature vector for entire song: (133, 30)
shape of segment feature vector: (30,)
(133, 30)
i_remember, sr = librosa.load('/Users/benjamindykstra/Music/iTunes/Deadmau5/Random Album Title/07 I Remember.m4a')
i_remember_segmented = segment_onset(i_remember)
feature_vec_remember = extract_features([{'song_name': '07 I Remember.m4a', 'data': i_remember_segmented['data']}])
Processing 07 I Remember.m4a with 1852 segments
shape of feature vector for entire song: (1852, 30)
shape of segment feature vector: (30,)
These two songs are very different
ipd.Audio(np.concatenate(i_remember_segmented['data'][:30]), rate= sr)
ipd.Audio(np.concatenate(rock_n_roll['data'][:20]), rate= sr)
We need to scale the features to a common range, the feature ranges differ wildly
col_names = ['energy'] + ["mfcc_" + str(i) for i in xrange(19)] + ['zero_crossing_rate', 'spectral_centroid'] + ['spectral_contrast_band_' + str(i) for i in xrange(7)] + ['bpm']
rnr = pd.DataFrame(feature_vec_rock, columns = col_names)
i_remember_df = pd.DataFrame(feature_vec_remember, columns = col_names)
min_max_scaler = sklearn.preprocessing.MinMaxScaler(feature_range=(-1, 1))
rnr_scaled = pd.DataFrame(min_max_scaler.fit_transform(feature_vec_rock), columns = col_names)
i_remember_scaled = pd.DataFrame(min_max_scaler.fit_transform(feature_vec_remember), columns = col_names)
features_scaled = pd.DataFrame(np.vstack((rnr_scaled, i_remember_scaled)), columns = col_names)
rnr_scaled.head()
| energy | mfcc_0 | mfcc_1 | mfcc_2 | mfcc_3 | mfcc_4 | mfcc_5 | mfcc_6 | mfcc_7 | mfcc_8 | ... | zero_crossing_rate | spectral_centroid | spectral_contrast_band_0 | spectral_contrast_band_1 | spectral_contrast_band_2 | spectral_contrast_band_3 | spectral_contrast_band_4 | spectral_contrast_band_5 | spectral_contrast_band_6 | bpm | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | -1.000000 | 0.122662 | 1.000000 | -0.516018 | 1.000000 | 0.602426 | 1.000000 | 1.000000 | 1.000000 | 0.540636 | ... | -1.000000 | -1.000000 | 0.827903 | -1.000000 | -0.962739 | -1.000000 | -1.000000 | -1.000000 | -0.538654 | -0.503759 |
| 1 | -0.242285 | -0.648073 | 0.381125 | -0.786313 | -0.091164 | -0.080649 | -0.601857 | -0.673427 | -0.444300 | -0.700703 | ... | 0.604015 | 0.709584 | 0.099070 | -0.187083 | -0.375223 | -0.307743 | -0.114691 | -0.157464 | 0.903511 | -0.250000 |
| 2 | -0.067639 | -0.850079 | 0.421647 | -0.732783 | -0.226694 | -0.404820 | -0.733511 | -0.860285 | -0.528783 | -0.503516 | ... | 0.781001 | 0.850525 | 0.758635 | -0.287418 | -0.213330 | -0.196650 | -0.161395 | 0.109064 | 0.427987 | -0.503759 |
| 3 | -0.433760 | -0.969241 | 0.401582 | -0.620675 | -0.046703 | 0.055861 | -0.502694 | -0.516944 | 0.055559 | -0.147803 | ... | 0.831207 | 0.924291 | 0.801980 | 0.226105 | -0.535366 | -0.160115 | 0.185044 | 0.142246 | 0.299663 | -0.503759 |
| 4 | -0.282242 | -0.686175 | 0.325491 | -0.689084 | -0.086337 | -0.026573 | -0.474765 | -0.471087 | -0.126714 | -0.212362 | ... | 0.496496 | 0.731278 | 0.755725 | 0.126388 | 0.024655 | -0.247040 | 0.625841 | 0.129373 | 0.113422 | -0.503759 |
5 rows × 30 columns
i_remember_scaled.head()
| energy | mfcc_0 | mfcc_1 | mfcc_2 | mfcc_3 | mfcc_4 | mfcc_5 | mfcc_6 | mfcc_7 | mfcc_8 | ... | zero_crossing_rate | spectral_centroid | spectral_contrast_band_0 | spectral_contrast_band_1 | spectral_contrast_band_2 | spectral_contrast_band_3 | spectral_contrast_band_4 | spectral_contrast_band_5 | spectral_contrast_band_6 | bpm | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.058494 | -0.647307 | 0.539341 | -0.121477 | 0.541506 | 0.437682 | -0.272703 | 0.223814 | -0.016933 | -0.048312 | ... | -0.114140 | 0.491343 | 0.292913 | 0.271760 | 0.192199 | -0.773597 | -0.625672 | -0.067422 | 0.317499 | -0.676113 |
| 1 | -0.005999 | -0.534543 | -0.160968 | -0.374121 | 0.505839 | 0.547995 | -0.180246 | 0.333693 | -0.098430 | 0.029649 | ... | -0.273774 | 0.318984 | 0.266204 | -0.026715 | -0.369555 | -0.694350 | -0.538811 | -0.494475 | 0.247816 | -0.676113 |
| 2 | -0.014792 | -0.465639 | -0.168007 | -0.570869 | 0.449955 | 0.559676 | -0.168267 | 0.279917 | -0.095737 | -0.053418 | ... | -0.327139 | 0.187170 | 0.507119 | 0.038864 | -0.463672 | -0.728928 | -0.451278 | -0.269847 | 0.223124 | -0.676113 |
| 3 | 0.127275 | -0.410650 | 0.045166 | -0.534741 | 0.485562 | 0.635807 | -0.145189 | 0.292996 | -0.003948 | 0.145229 | ... | -0.474190 | 0.109161 | 0.216147 | -0.372901 | -0.184409 | -0.732067 | -0.453334 | -0.383937 | 0.103847 | -0.676113 |
| 4 | 0.099671 | -0.368250 | 0.332703 | -0.435360 | 0.505144 | 0.570220 | -0.128529 | 0.181684 | -0.068506 | -0.032707 | ... | -0.539708 | 0.116126 | 0.209937 | -0.236042 | -0.115957 | -0.544722 | -0.496779 | -0.378822 | -0.068973 | -0.676113 |
5 rows × 30 columns
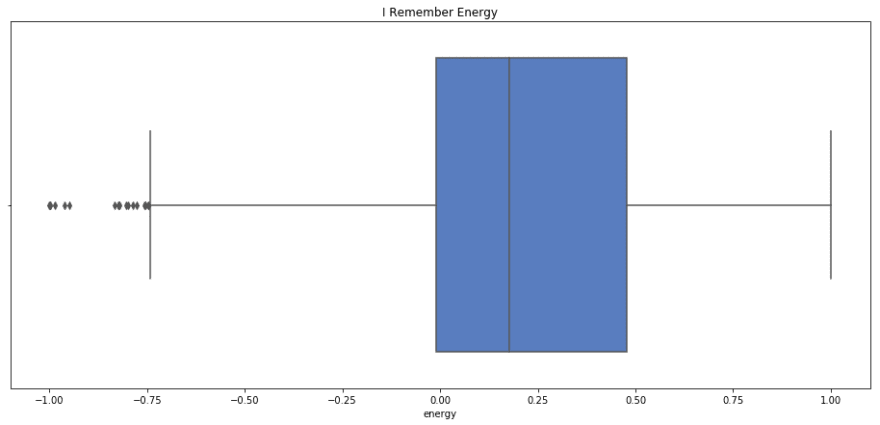
Lets take a look at the descriptive statistics for the energy
sns.boxplot(x=i_remember_scaled.energy, palette='muted').set_title('I Remember Energy');
plt.show();
print i_remember_scaled.energy.describe()
sns.boxplot(rnr_scaled.energy).set_title('Rock n Roll Energy');
plt.show();
print rnr_scaled.energy.describe()
count 1852.000000
mean 0.184555
std 0.373220
min -1.000000
25% -0.009499
50% 0.176136
75% 0.478511
max 1.000000
Name: energy, dtype: float64
count 133.000000
mean 0.354920
std 0.391389
min -1.000000
25% 0.117536
50% 0.439199
75% 0.639228
max 1.000000
Name: energy, dtype: float64
I remember has a lower mean and median energy, but similar spread to Rock n Roll. I'd say that this fits, as I Remember has almost a melancholic energy, where as Rock n Roll really makes you to get up and move.
What about the zero crossing rate and BPM?
Since zero crossing rate and bpm correlate pretty highly with percussive events, I'd predict that the song with the higher BPM will have a higher zero crossing rate
print 'Rock n Roll average BPM: {}'.format(rnr.bpm.mean())
print 'Rock n Roll average Crossing Rate: {}'.format(rnr.zero_crossing_rate.mean())
print 'I Remember average BPM: {}'.format(i_remember_df.bpm.mean())
print 'I Remember average Crossing Rate: {}'.format(i_remember_df.zero_crossing_rate.mean())
Rock n Roll average BPM: 150.784808472
Rock n Roll average Crossing Rate: 0.14643830815
I Remember average BPM: 136.533708743
I Remember average Crossing Rate: 0.0362864360563
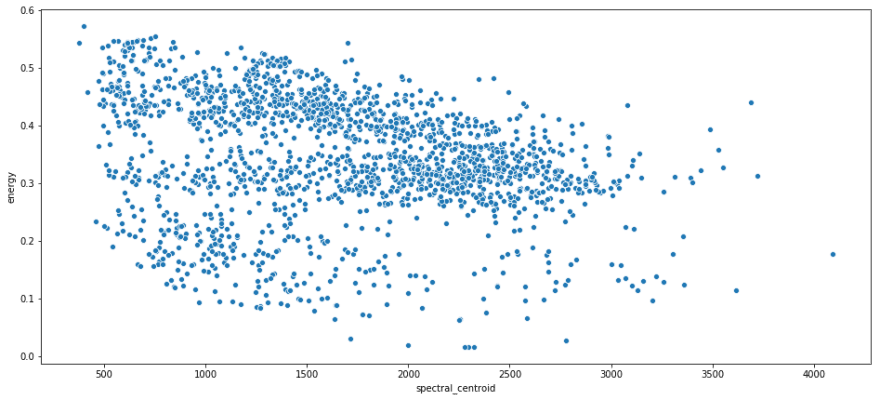
Some scatterplots with spectral centroid on the x axis, and energy on the y axis.
sns.scatterplot(x = rnr.spectral_centroid, y = rnr.energy);
plt.show();
sns.scatterplot(x = i_remember_df.spectral_centroid, y = i_remember_df.energy );
plt.show();
Recall that spectral centroid is where the spectral 'center of mass' is for a given segment. That means that it's picking out the dominant frequency for a segment. I like this because it shows that there's not real relation between the frequency of a segment and its energy. They are both contributing unique information.
build labels and cluster using k means!
song_labels = np.concatenate([np.full((label_len), i) for i, label_len in enumerate([len(rnr), len(i_remember_df)])])
model = sklearn.cluster.KMeans(n_clusters=3)
labels = model.fit_predict(features_scaled)
plt.scatter(features_scaled.zero_crossing_rate[labels==0], features_scaled.energy[labels==0], c='b')
plt.scatter(features_scaled.zero_crossing_rate[labels==1], features_scaled.energy[labels==1], c='r')
plt.scatter(features_scaled.zero_crossing_rate[labels==2], features_scaled.energy[labels==2], c='g')
plt.xlabel('Zero Crossing Rate (scaled)')
plt.ylabel('Energy (scaled)')
plt.legend(('Class 0', 'Class 1', 'Class 2'))
<matplotlib.legend.Legend at 0x13f054f10>
unique_labels, unique_counts = np.unique(model.predict(rnr_scaled), return_counts=True)
print unique_counts
print 'cluster for rock n roll: ', unique_labels[np.argmax(unique_counts)]
[29 9 95]
cluster for rock n roll: 2
unique_labels, unique_counts = np.unique(model.predict(i_remember_scaled), return_counts=True)
print unique_counts
print 'cluster for I remember: ', unique_labels[np.argmax(unique_counts)]
[396 877 579]
cluster for I remember: 1
I suspect that zero crossing rate and energy are not what the determining factors are for a cluster :)
We can actually listen to the segments that were assigned certain labels
Note that these aren't necessarily consecutive segments
First lets look at I remember
i_remember_clusters = model.predict(i_remember_scaled)
label_2_segs = i_remember_segmented['data'][i_remember_clusters==2]
label_1_segs = i_remember_segmented['data'][i_remember_clusters==1]
label_0_segs = i_remember_segmented['data'][i_remember_clusters==0]
Almost all of theses have some of the vocals in them
ipd.Audio(np.concatenate(label_2_segs[:50]), rate = sr)
These are the lighter segments, mostly just synths
ipd.Audio(np.concatenate(label_1_segs[:50]), rate = sr)
0 labels seem to be the heavy bass and percussive parts
ipd.Audio(np.concatenate(label_0_segs[:50]), rate = sr)
Now Rock n Roll
rnr_clusters = model.predict(rnr_scaled)
rock_label_2_segs = rock_n_roll['data'][rnr_clusters==2]
rock_label_1_segs = rock_n_roll['data'][rnr_clusters==1]
rock_label_0_segs = rock_n_roll['data'][rnr_clusters==0]
Again, higher frequencies, vocals included. A lot of consecutive segments included in this class.
ipd.Audio(np.concatenate(rock_label_2_segs[10:40]), rate = sr)
<audio controls="controls" >
Your browser does not support the audio element.
</audio>
Lighter sounds, minor key vocals, part of final drum solo
ipd.Audio(np.concatenate(rock_label_1_segs), rate = sr)
<audio controls="controls" >
Your browser does not support the audio element.
</audio>
All John Bonham here (only drums). Similar to how in I remember label 0 corresponded to the heavy bass
ipd.Audio(np.concatenate(rock_label_0_segs), rate = sr)
<audio controls="controls" >
Your browser does not support the audio element.
</audio>
Conclusion
We've used two very different songs to build vectors of spectral and rhythmic features. We then examined how those features related to each other with boxplots, scatterplots and descriptive statistics. Using those features, we have clustered different segments of the songs together to compare how the different clusters sound together.
More exploration is needed to figure out how to assign a feature value for an entire song that is representative. With more work doing that, it would then be possible to get summary features for entire songs. More on this later!
The rest of this is just some undirected exploring of different features
print rnr_scaled[rnr_clusters==0]['spectral_centroid'].describe()
print rnr_scaled[rnr_clusters==1]['spectral_centroid'].describe()
print rnr_scaled[rnr_clusters==2]['spectral_centroid'].describe()
count 9.000000
mean -0.360693
std 0.250294
min -1.000000
25% -0.370240
50% -0.280334
75% -0.260073
max -0.148394
Name: spectral_centroid, dtype: float64
count 29.000000
mean 0.066453
std 0.363603
min -0.483240
25% -0.211871
50% 0.012854
75% 0.156281
max 0.814435
Name: spectral_centroid, dtype: float64
count 95.000000
mean 0.354971
std 0.261067
min -0.669203
25% 0.218433
50% 0.318239
75% 0.427016
max 1.000000
Name: spectral_centroid, dtype: float64
i_remember_df['mfcc_2'].plot.hist(bins=20, figsize=(14, 5))
<matplotlib.axes._subplots.AxesSubplot at 0x139127290>
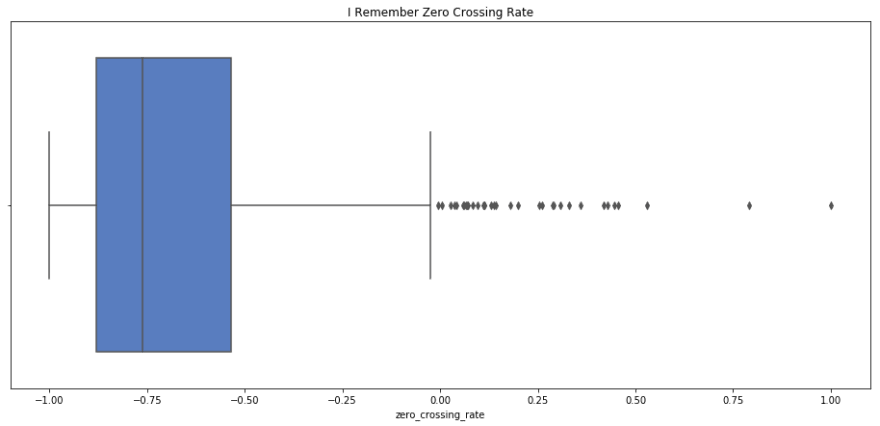
sns.boxplot(x=i_remember_scaled.zero_crossing_rate, palette='muted').set_title('I Remember Zero Crossing Rate');
plt.show();
print i_remember_scaled.zero_crossing_rate.describe()
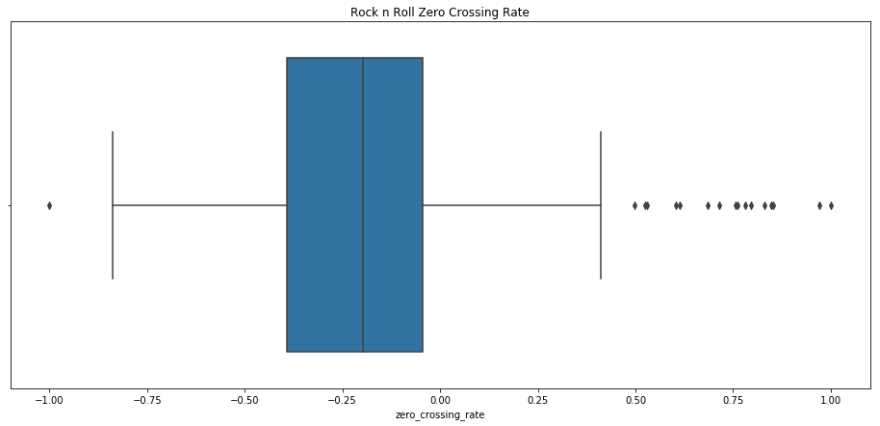
sns.boxplot(rnr_scaled.zero_crossing_rate).set_title('Rock n Roll Zero Crossing Rate');
plt.show();
print rnr_scaled.zero_crossing_rate.describe()
count 1852.000000
mean -0.683760
std 0.255792
min -1.000000
25% -0.880912
50% -0.762325
75% -0.535427
max 1.000000
Name: zero_crossing_rate, dtype: float64
count 133.000000
mean -0.152444
std 0.421004
min -1.000000
25% -0.393116
50% -0.198213
75% -0.045042
max 1.000000
Name: zero_crossing_rate, dtype: float64
print rnr.zero_crossing_rate.describe()
print i_remember_df.zero_crossing_rate.describe()
count 133.000000
mean 0.146438
std 0.072255
min 0.000977
25% 0.105133
50% 0.138583
75% 0.164871
max 0.344226
Name: zero_crossing_rate, dtype: float64
count 1852.000000
mean 0.036286
std 0.025857
min 0.004319
25% 0.016357
50% 0.028345
75% 0.051281
max 0.206489
Name: zero_crossing_rate, dtype: float64
print rnr.bpm.describe()
print i_remember_df.bpm.describe()
count 133.000000
mean 150.784808
std 31.793864
min 86.132812
25% 135.999178
50% 135.999178
75% 172.265625
max 287.109375
Name: bpm, dtype: float64
count 1852.000000
mean 136.533709
std 7.140772
min 112.347147
25% 135.999178
50% 135.999178
75% 135.999178
max 258.398438
Name: bpm, dtype: float64
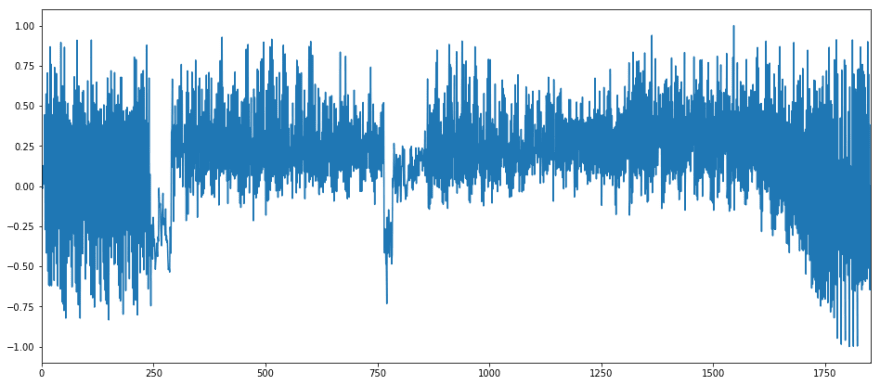
# rnr_scaled['energy'].plot();
i_remember_scaled['energy'].plot();
# rnr_scaled['zero_crossing_rate'].plot();
# rnr_scaled['spectral_centroid'].plot();
# rnr_scaled['mfcc_4'].plot();
plt.show()
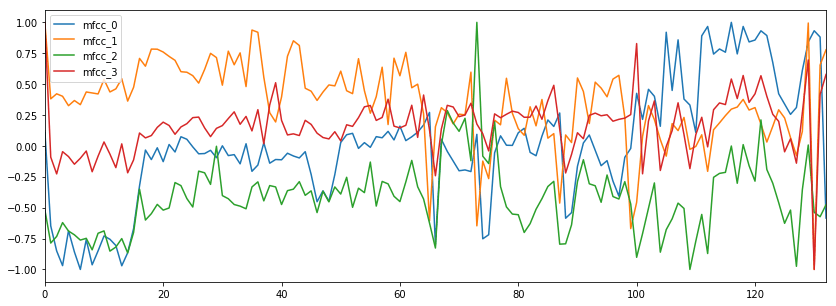
rnr_scaled[['mfcc_' + str(i) for i in xrange(4)]].plot();
plt.show();
sns.scatterplot(x=rnr_scaled['energy'], y = rnr_scaled['bpm'])
<matplotlib.axes._subplots.AxesSubplot at 0x131c69ad0>
sns.pairplot(rnr_scaled[['mfcc_' + str(i) for i in xrange(5)]], palette='pastel')
<seaborn.axisgrid.PairGrid at 0x15f503c10>





Top comments (0)