Follow Me, Shout Out, or Give Thanks!
Please 💖 this article. a small thing to keep me motivated =)
Twitter: @djjasonclark
Linkedin: in/clarkngo
Description
Given the availability time slots arrays slots1 and slots2 of two people and a meeting duration, return the earliest time slot that works for both of them and is of duration.
If there is no common time slot that satisfies the requirements, return an empty array.
Example 1
Input: slots1 = [[10,50],[60,120],[140,210]], slots2 = [[0,15],[60,70]], duration = 8
Output: [60,68]
Example 2
Input: slots1 = [[10,50],[60,120],[140,210]], slots2 = [[0,15],[60,70]], duration = 12
Output: []
Scenario
Today, your two coworkers need to meet for a specific time duration at the earliest available time. Both of them gave you a list of open slots in their day. You are tasked to find overlapping slots (open slot of co-worker A and open slot co-worker B) the would allow them to have a meeting given the time duration of the meeting.
Logic
Look at co-worker A available slot AND compare it with co-worker B available slot.
If the available slot range is not within the meeting time duration, look for the next available slot of a co-worker.
Question: Which co-worker's next available slot should we look at first to compare with the other co-worker's current available slot?
Answer: The co-worker, with the lower end time for its current available slot compared to the other co-worker's end time for its current available slot, is the one we should check for the next available slot.
Algorithm: Two Pointer Technique
- Use of two pointers in a loop.
- Helps reduce the time complexity of O(n3) or O(n2) to O(n) with just one loop.
Pseudocode
Sort the
slots1andslots2array in ascending order of the starting time. Use Arrays.sort() withComparatorin the 2nd parameter.Initialize two pointers at index 0.
While pointer for the length of
slots1is less than the length ofslots1and pointer for the length ofslots2is less than the length ofslots2.
a. Initialize/reinitialize two arrays to hold the current slot for each co-worker.
b. Initialize/reinitialize two integers: 1) to store the max start time between two co-worker's current available slots. 2) to store the minimum end time between two co-worker's current available slots.
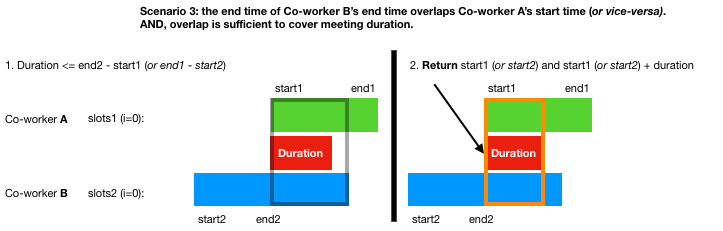
c. If duration is within the range of max start time and min end time, then return start time and start time + duration.
Else if end time of co-worker A less than the end time of co-worker B, then increment co-worker A's pointer.
Else if end time of co-worker B less than the end time of co-worker A, then increment co-worker B's pointer.
Else increment both co-workers A and B's pointers.Return empty array. No overlapping slots the would allow the co-workers to have a meeting given the time duration of the meeting.
Scenarios
Scenario 1: the end time of Co-worker A’s end time overlaps Co-worker B’s start time.
HOWEVER, overlap is NOT sufficient to cover meeting duration.

Scenario 2: the end time of Co-worker B’s end time overlaps Co-worker A’s start time.
HOWEVER, overlap is NOT sufficient to cover meeting duration.

Scenario 3: the end time of Co-worker B’s end time overlaps Co-worker A’s start time (or vice-versa).
AND, overlap is sufficient to cover meeting duration.
Code
class Solution {
public List<Integer> minAvailableDuration(int[][] slots1, int[][] slots2, int duration) {
Arrays.sort(slots1, (a,b)-> a[0]-b[0]);
Arrays.sort(slots2, (a,b)-> a[0]-b[0]);
int p1 = 0;
int p2 = 0;
while (p1 < slots1.length && p2 < slots2.length) {
int[] curr1 = slots1[p1];
int[] curr2 = slots2[p2];
int start = Math.max(curr1[0], curr2[0]);
int end = Math.min(curr1[1], curr2[1]);
if (end - start >= duration)
return Arrays.asList(start,start+duration);
else if (curr1[1] < curr2[1]) p1++;
else if (curr2[1] < curr1[1]) p2++;
else {
p1++;
p2++;
}
}
return new ArrayList<>();
}
}

![Cover image for Logic Explained: Meeting Scheduler - Leetcode [Java] using Two Pointers](https://media2.dev.to/dynamic/image/width=1000,height=420,fit=cover,gravity=auto,format=auto/https%3A%2F%2Fdev-to-uploads.s3.amazonaws.com%2Fuploads%2Farticles%2F79ftek9piie0934s1kzx.png)

Top comments (0)