What is the N-Queens-Puzzle?
Following this Wiki link to the 8-Queens-Puzzle one quickly understands the simple puzzle imposed. Summarizing, the objective is to place the N-Queens on a (NxN) board, so that no queen is attacked by another - vertically, horizontally or diagonally (just like chess).
(One) Solution:
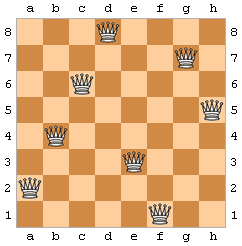
Simple to understand, yet exponentially hard to solve.
Problem-Formulation
We now understand our problem - great - but the question here is:
How will we solve it? - What is the best approach for most plays?
- Will we try for each queen every not occupied position and verify its validity? - in other words, brute force our way to the solution.
- Will we place a queen and immediately cross out all the positions it attacks and try to place the next one on all the valid positions left?
- Do we even need to consider all the valid positions left?
- For the first queen, the board is empty - where do we try to place the very first one since all positions are valid? Everywhere?
The list goes on and on. As I'm trying to expose here, there are many different and valid ways to formulate the problem and find a solution.
But some are better than others. Way better.
Obviously the first approach always comes down to brute-force. But this is where our understanding and perspective of the problem comes into play. By brute-forcing the various possible positions to place a queen we are mistakenly trying solution paths that - if we give it a little thought - are, from the very first step, unsolvable.
Just to give you a little taste
Bear with me in this line of thought:
Given the way a queen attacks the various positions on a board, does it make any sense to place another on the same row? or the same column? or even, the same diagonal? No, the answer is no, it does not make sense, because we know immediately that this positions are invalid once we place a queen - we need not even think of this possibilities.
Even more, since we now know there is no point in placing a queen on the same row, column or diagonal as another, we know exactly where to place the very first queen. No, we do not have N * N (reads N times N) possibilities for the first queen, actually, we only have N, on the very first column. And the same goes for the next queen - meaning, there is no point in trying to place a queen somewhere else than the leftmost free column, since every column will have exactly one and only one queen.
This perspective (or, formally, problem-formulation) will immensely reduce the possible solution path's to take - therefore, will be much faster and efficient
Conclusions
The way we tackle a problem, starting with how well we understand it, will greatly affect the outcome of our solving. This is actually tangible with some AI resources:
How well does an algorithm preform given a certain problem-formulation?
How much time, tried possibilities and different solution path's will it expand to reach a solution?
I have implemented (here) in python all of the above problem-formulations and some more, so that anyone can try and verify it by themselves.
I purposely implemented them with a blind-search, the least efficient way to find a solution for a problem we know so well - to show how well it will preform compared with poor/better problem-formulations.
Regards
I hope you enjoyed the post and actually give my comparator tool a try to see it in action by yourself! Please give me feedback or implement new ideas of problem-formulations!
See you next time,
Diogo from Portugal



Top comments (1)
This is my first post, all feedback is welcomed!