It's been a while since the last post in this series. I was very busy with other things, but I'm back! Yes! 😁 In this post, we will continue to learn a new data structure and how to implement it. 👨💻👩💻
💭 "Falling in love with code means falling in love with problem solving and being a part of a forever ongoing conversation. To be a computer programmer does not mean to live in isolation and solitude, but rather the exact opposite." - Kathryn Barrett
Outline
- What is a Heap?
- Basic concepts
- The main operations and properties.
Let's start to work! 😃
Pre-requisite : Tree
If you haven't read tree and binary search tree, I recommend you check it out first!
- What is a Heap? 🧐
If you've seen how the heap structure organizes values, you might think that there are some similarities to the tree structure. Yes, indeed. Basically, we can define a heap structure as a special full binary tree structure where each element has exactly two children, the only exception can be the deepest level.
One important thing to keep in mind about this structure is that there are two types of the heap and the differences between them are related to the property of storing a value, which can be:
- Max-heap: The root element has the maximum value and the value for every element is equal or greater than the value in the node’s children.
Figure 1: Max-heap representation.
- Min-heap: Here we have the opposite side because the root element has the minimum value and the value for every element is equal to or less than the value in the node’s children.
Figure 2: Min-heap representation.
As we can see, every element can be actually called as the root of its own sub-heap. For instance, using min-heap example given above we can say that the value 8 is the root of 7 and 3 sub-heap.
Figure 3: Example of sub-heap.
After describing the basics and understanding what the heap is, how do we create this data structure? First things first, let's start building the constructor.
So, you may be thinking and assuming based on the last post about tree structure that we could implement a simple class that contains left and right elements, right? 🧐
You are absolutely right! 😃 We can certainly implement it that way, however, there is another and better approach that we can use to create an efficient way of implementing it.
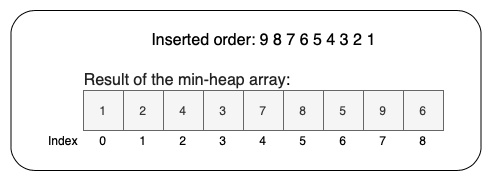
Instead of creating these elements, we can use an array to store all the heap values, simple right? In this way, we just need to store all the values top to bottom, left to right, and that's it! Using this approach, we can know that the fifth value in the array will be the fifth value in the heap, for instance.
Let's use the min-heap example used above and take a look at the following image:
Figure 3: Array-heap representation.
The use of array indexes can describe the parent-child structure. But, wait! ✋ What that's mean? 🤔 Looking at the element, we can get the left child element by Arr[(2*i)+1] that returns the value. And the parent and right element? Let's take a look below:
- Index of element = i
- Returns the left child element = Arr[(2*i)+1]
- Returns the right child element = Arr[(2*i)+2]
- Returns the parent element = Arr[i/2]
For example, let's use the value X in the array, which is the third element of the structure. To get the parent value, we just have to get the index value and divided it by 2. Simple right? That said, understanding how we can access these values will be extremely important in the next function in the heap structure.
Now that we're on the same page, let's move on and put everything that we've learned into our code. First, we need to create the skeleton of our heap class.
class Heap {
constructor() {
this.list = [];
}
...
}
Basic operations
Okay, now that we already know how to build the heap structure let's diving into the main operations.
Talk is cheap. Show me the code! 😁
◼️ Insert
To insert a new element it is necessary to find the first available space in the structure looking for an empty spot from top to bottom and left to right order.
After that, it may be necessary to rearrange the structure, this process will compare the value inserted with the parent value based on the type of heap. The elements should be swap if not follow the heap property and continue to bubble until finding the right spot in the structure.
In this function, we might have to make a comparison at each level of the structure and then swap the elements until the root element. Every time a new value goes up it takes O(1) time. So, the worst-case time complexity is O(nlg n) because we insert the value at the end of the heap and traverse up.
insert(value){
this.list.push(value);
var childrenIndex = this.list.indexOf(value);
while(this.hasParentByIndex(childrenIndex)){
if(this.shouldSwap(childrenIndex, this.getParentByIndex(childrenIndex))){
this.swapElements(childrenIndex, this.getParentByIndex(childrenIndex));
childrenIndex = this.getParentByIndex(childrenIndex);
} else{
break;
}
}
}
⚡️ If you would like to learn others functions that I implemented you can access all the code just clicking here.
◼️ Deletion
In the Heap, we remove the root element of the structure and then replace it with the last value added. As you may be thinking, the new root element might probably not be in the right position. To solve this problem it is necessary to call the heapify function, which is the most critical operation in this structure where it reorganizes the values until the heap property is satisfied.
removeFromTop(){
if(this.isEmpty())
throw new Error('The Heap is Empty');
if(this.getSize() == 1){
this.list.pop();
} else {
this.swapToRemove();
this.heapify();
}
}
swapToRemove(){
this.swapElements(this.list.length - 1, 0);
this.list[this.list.length - 1] = null;
this.list = this.list.filter(function (element) {
return element != null;
});
}
swapElements(childrenIndex, parentIndex) {
const tmp = this.list[parentIndex];
this.list[parentIndex] = this.list[childrenIndex];
this.list[childrenIndex] = tmp;
}
Using a top-down approach, this function will bubble it down comparing the new root element and the left and right child, then swap elements according to the type of heap and repeat the process until the new root element finds a valid spot and the heap property has been satisfied.
Let's see how we can put these words in a code.
heapify(index=0){
let left = this.getLeftChildrenIndex(index),
right = this.getRightChildrenIndex(index),
largest = index;
if(!this.list[left]) return;
if(this.shouldSwap(left, largest) ){
largest = left;
}
if(this.shouldSwap(right, largest) ){
largest = right;
}
if(largest !== index){
[this.list[largest],this.list[index]] = [this.list[index],this.list[largest]];
this.heapify(largest);
}
}
We can say that the main point of heapify function is to make sure that the structure follows the heap propriety by comparing the elements and the child elements.
The time complexity for swap element in each level is O(1) and the worst-case time is O(lg n) and it depends on how far an element can move down, which is related to the height of the heap. In the worst case, the element might go down all the way to the leaf level.
⚡️ If you would like to learn others functions that I implemented you can access all the code just clicking here.
◼️ Merge heaps
To merge two existing heap into a single one can be done by all values moved from the smallest heap to the largest using the insert function. However isn't the best way because involves moving N items and rearranging at cost 0(log n), giving an overall time complexity of O(nlog n).
The best approach is just to concatenate the values of two heaps and then use heapify algorithm, as we can see below:
mergeHeaps(heap){
var array = []
for (var i = 0; i < this.size; i++) {
array[i] = this.list[i];
}
for (var i = 0; i < heap.size; i++) {
array[this.size + i] = heap.list[i];
}
var total = this.size + heap.size;
this.list = array
for (var i = total / 2 - 1; i >= 0; i--) {
this.heapify(i)
}
}
We are done 🙌
That's all, folks! I see you arround and wash your hands and use masks. 😁😷
Code: https://github.com/FernandoBLima/data-structures
We finished our discussion about Heap structure. 🙌
If you found something I miss out or find this article helpful, feel free to let me know. 😁







Top comments (0)