In this entry I want to share you, how to solve the water jug riddle using Javascript, by the way a curious fact, this problem is featured in the film Die Hard. So, the riddle is:
You have 2 jugs, 5 and 3 liters of capacity respectively, without any measurement mark, in addition you have an unlimited water source that allows you to fill the jugs with water. Exactly 4 liters of water is required in one of the jugs.
Note: The same problem is explained in this entry and is implemented in Prolog (Spoiler: is in spanish).
First of all, we should answer the following question, How would we solve this manually?
In order to measure the 4 liters required, a set of steps must be executed, we suppose that, the initial state is 0 liters of water in the large and small jug.
2. Once the 5-liter jug is full, pour the content of the large jug into the small one, resulting in 2 and 3 liters of water; now the small jug is full.
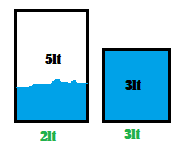
4. Pour the contents of the large jug into the small jug. The large jug contains 0 liters of water and 2 liters the small jug.
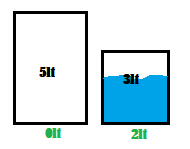
6. Pour the content of the large jug into the small one where there is 2 lt of water. Since it only takes one liter to fill the small jug and the large jug contains 5 lt of water. As you pass from the large jug into the small jug, 4 liters of water results in the large jug.

Finally, in this step the problem has been solved in 6 steps, it should be mentioned that this is not the unique solution, since there are more, for example, you can start by filling the small jug (3lt).
Implementation in JS
To represent each state of the jugs, I'm going to use an object, it has two properties, small and large, of type integer.
const state = { small: 0, large: 0 }
In the following code, 4 functions are written to modify the jugs states.
const MAX_LARGE = 5
const MAX_SMALL = 3
const fillJug = (jugs, key = 'large', max = MAX_LARGE) => ({ ...jugs, [key]: max })
const emptyJug = (jugs, key = 'large') => ({ ...jugs, [key]: 0 })
const largeToSmall = ({ large, small }) => {
const quantityNeededToFillSmall = MAX_SMALL - small
return {
large: large > quantityNeededToFillSmall
? large - quantityNeededToFillSmall : 0,
small: large > quantityNeededToFillSmall
? small + quantityNeededToFillSmall : small + large
}
}
const smallToLarge = ({ large, small }) => {
const quantityNeededToFillLarge = MAX_LARGE - large
return {
large: small > quantityNeededToFillLarge
? small - quantityNeededToFillLarge : 0,
small: small > quantityNeededToFillLarge
? large + quantityNeededToFillLarge : small + large
}
}
const isRepeated = (path, { small, large }) =>
!!path.find(x => x.small === small && x.large === large)
The first 2 lines are constants to define the maximum capacity of jugs.
- fillJug, this function will modify the jugs state, filling one of them by its key, both jugs and key are passed as parameters, refer to explanation 1 and 5 of this entry.
- emptyJug, it'll empty a jug, put state in 0, small or the large one, as point 3 of the previous explanation.
-
largeToSmall, pour the content of the large jug into the small one.
- quantityNeededToFillSmall, is self explanatory.
- large, if the quantity of water in the large jug is greater than quantity needed to fill the small one, subtract the quantity of water from the large jug and the quantity needed to fill the small one (large - quantityNeededToFillSmall), it means not all the content of the large jug will be poured into the small one. Otherwise, it'll be zero, because it means that all the content of the large jug are poured into the small one.
- small, if the quantity of water in the large jug is greater than quantity needed to fill the small one means, the small jug doesn't have the capacity to store all the content of the large jug, so is added just the quantity of the small jug and the quantity needed to fill it (small + quantityNeededToFillSmall). Otherwise, all of the content from the large jug will be poured into the small one (small + large).
- smallToLarge, pour the content of the small jug into the large one. The rest is similar to the previous explanation, but in reverse.
- isRepeated, will check if the new state already exists in path.
To find the path to the solution, Breadth-First Search (BFS) is proposed, because is the most efficient algorithm to find the shortest path, this algorithm begins from the root and goes through each node by levels instead of branches as Deep-First Search (DFS) does, using a queue to temporarily store nodes.
BFS is implemented to find the shortest path.
function getShortestPath(start, target) {
const queue = []
const path = []
path.push(start)
queue.push(path)
while (queue.length) {
const lastPath = queue.shift()
const lastState = lastPath[lastPath.length - 1]
if (target === lastState.large)
return lastPath
const states = new Set([fillJug(lastState), fillJug(lastState, 'small', MAX_SMALL),
largeToSmall(lastState), smallToLarge(lastState), emptyJug(lastState), emptyJug(lastState, 'small')])
for (let item of states) {
if (!isRepeated(lastPath, item)) {
const newPath = [...lastPath]
newPath.push(item)
queue.push(newPath)
}
}
}
return null
}
path = getShortestPath(state, 4)
console.log(path)
- getShortestPath, receives two parameters, the first one is the initial state of the jugs, and the second one is the final quantity needed.
- Declare an array (queue), which will be used as a queue to store the shortest path.
- Declare an array (path), to store the selected states.
- Add the initial state as the first element of the path array, path.push(start), then this path is added to the queue.
-
While data exists in the queue, while(queue.length), the following instructions are executed.
- The first element of the queue is removed (queue.shift()), and stored in lastPath variable.
- The last state is selected from the last path array (lastState = lastPath[lastPath.length - 1]).
- If the quantity in the large jug (last state) selected is equal to target value that you are looking for, it returns the list of obtained state (shortest path) (return lastPath). Otherwise it'll continue.
- We add the possible states that can be generated from the last one, to a Set data structure.
- For each state obtained in the previous step, the next instructions are executed.
- It's reviewed that the generated state isn't yet included in the path (solution path).
- In case the previous condition is met, create a new list (new path) with the states of the last path.
- In this new path is added the new state of the jugs (newPath.push(item)), afterwards the new path is added to queue.
- Finally, if during the repetitive cycle the target state is not found, it returns null.
When executing the previous code, the following is printed in console.
path = getShortestPath(state, 4)
console.log(JSON.stringify(path, null,'\t'))
// console output
[
{ "large": 0, "small": 0 },
{ "large": 5, "small": 0 },
{ "large": 2, "small": 3 },
{ "large": 2, "small": 0 },
{ "large": 0, "small": 2 },
{ "large": 5, "small": 2 },
{ "large": 4, "small": 3 }
]
I hope you've enjoyed!.
It's my second blog, written entirely in English (I'm not a native speaker), maybe you've already realized, so sorry for the misspellings!, please If you have any recommendation, or comment you can leave in the comments section.
Stay safe and thanks for reading!





Top comments (2)
Nice post, I like how it presents a problem and a solution. Thanks for sharing this fun problem with me!
You're welcome!
Some comments may only be visible to logged-in visitors. Sign in to view all comments.