String matching (KMP algorithm)

#algorithms

The string matching problem also known as “the needle in a haystack is one of the classics. This simple problem has a lot of application in the areas of Information Security, Pattern Recognition, Document Matching, Bioinformatics (DNA matching) and many more. Finding a linear time algorithm was a challenge, then came our father Donald Knuth and Vaughan Pratt conceiving a linear time solution in 1970 by thoroughly analysing the naive approach. It was also independently discovered by James Morris in the same year. The three published the paper jointly in 1977 and from that point on it is known as the Knuth-Morris-Pratt aka KMP Algorithm.

This is my first blog in the series and the approach I follow is I start with the basics then keep building on it till we reach the most optimised solution. I will be using Python for code snippets as it’s very much concise and readable. Here we go..

Problem statement:

To Find the occurrences of a word W within a main text T.
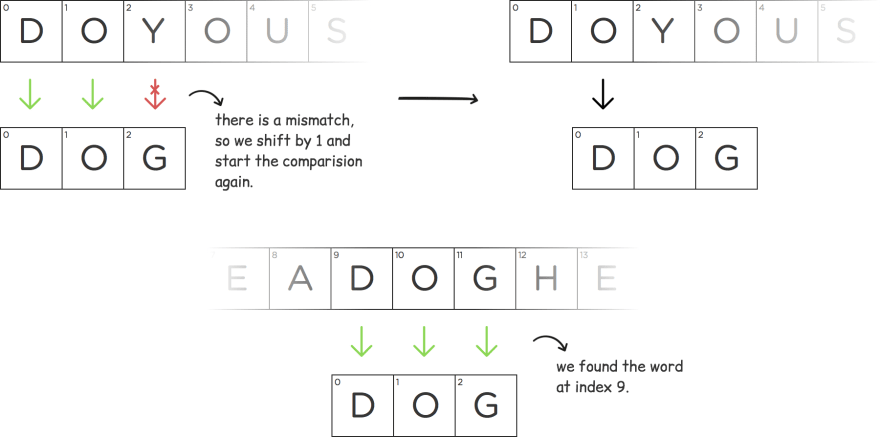
One naive way to solve this problem would be to compare each character of W with T. Every time there is a mismatch, we shift W to the right by 1, then we start comparing again. Let’s do it with an example:

T: DoYouSeeADogHere (it will be a case insensitive search for all examples)
W: dog

# Here is the working code of the naive approach.
def bruteSearch(W, T):
    # edge case check
    if W == "":
            return -1

    # getting the length of the strings
    wordLen = len(W)
    textLen = len(T)

    # i is the index of text T from where we will start comparing the
    # the word W
    i = 0

    # length of the subtext has to be equal to the length of the word,
    # so no need to check beyond (textLen - wordLen + 1)
    while i < (textLen - wordLen + 1):
        # we set match to false if we find a mismatch
        match = True

        for j in range(wordLen):
            if W[j] != T[i + j]:
                # A mismatch
                match = False
                break

        if match:
            # We found a match at index i
            print "There is a match at " + str(i)

        # incrementing i is like shifting the word by 1
        i += 1

    return -1

Time complexity of this naive approach is O(mn), where m and n are length of the word W and the text T respectively. Let’s see how can we make it better. Take another wacky example with all unique characters in W.
T: duceDuck
W: duck

As you can see in the above image, there is a mismatch at index 3. According to naive approach next step would be to shift W by 1. Since all letters in W are different, we can actually shift W by the index where mismatch occurred (3 in this case). We can say for sure there won’t be any match in between. I would recommend to try with some other similar example and check for yourself.
The idea is to find out how much to shift the word W when there is a mismatch. So far we have optimised the approach only for a special case where all characters in W are unique. Let’s take another bizarre example. This one is gonna be little tricky so brace yourself.

T: deadElephant
W: deadEye

Make sure you understand what green cells convey. I will be using a lot of them. In the above image the green cells in the left substring is equal to the green cells in the right substring. It is actually the largest prefix which is also equal to the suffix of the substring till index 4 of the word “deadeye”. Assume for now we have found it somehow, we will work on finding out largest prefix(green cells) later. Now let's see how it works by taking an abstract example.

str1 = str2 (green cells) and str2 = str3. When there is a mismatch after str2, we can directly shift the word till after str1 as you can see in the image. Green cells actually tell us the index from where it should start comparing next, if there is a mismatch.

I suppose you now understand if we find out green cells for every prefix of the word W, we can skip few unnecessary matches and increase the efficiency of our algorithm. This is actually the idea behind knuth-Morris-Pratt(kmp) algorithm.

In search of green cells

We will be using aux[] array to store the index. Unlike Naive algorithm, where we shift the word W by one and compare all characters at each shift, we use a value from aux[] to decide the next characters to be matched. No need to match characters that we know will match anyway. Let’s take yet another weird example.

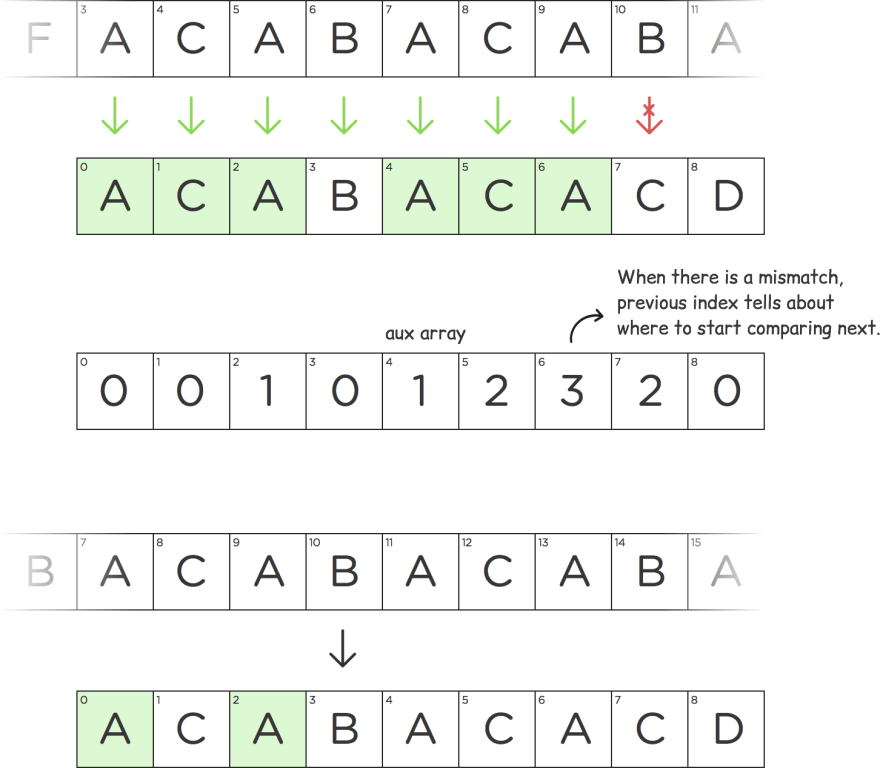
W: acabacacd

m and i define the state of our algorithm and signify that prefix of the word W before m is equal to the suffix for the substring till i-1 i.e W[0…m-1] = W[i-m…i-1]. For the above image state, 2(value of m) is stored in the aux[] array for the substring till index 4(i-1).

def createAux(W):
    # initializing the array aux with 0's
    aux = [0] * len(W)

    # for index 0, it will always be 0
    # so starting from index 1
    i = 1
    # m can also be viewed as index of first mismatch
    m = 0
    while i < len(W):
        # prefix = suffix till m-1
        if W[i] == W[m]:
            m += 1
            aux[i] = m
            i += 1
        # this one is a little tricky,
        # when there is a mismatch,
        # we will check the index of previous
        # possible prefix.
        elif W[i] != W[m] and m != 0:
            # Note that we do not increment i here.
            m = aux[m-1]
        else:
            # m = 0, we move to the next letter,
            # there was no any prefix found which 
            # is equal to the suffix for index i
            aux[i] = 0
            i += 1

    return aux

Following will be the aux array for the word acabacacd

Now let's use the above aux array to search the word acabacacd in the following text.

T: acfacabacabacacdk


W = "acabacacd"
T = "acfacabacabacacdk"

# this method is from above code snippet.
aux = creatAux(W)

# counter for word W
i = 0
# counter for text T
j = 0
while j < len(T):
    # We need to handle 2 conditions when there is a mismatch
    if W[i] != T[j]:
        # 1st condition
        if i == 0:
            # starting again from the next character in the text T
            j += 1
        else:
            # aux[i-1] will tell from where to compare next
            # and no need to match for W[0..aux[i-1] - 1],
            # they will match anyway, that’s what kmp is about.
            i = aux[i-1]
    else:
        i += 1
        j += 1
        # we found the pattern
        if i == len(W):
            # printing the index
            print "found pattern at " + str(j - i)
            # if we want to find more patterns, we can 
            # continue as if no match was found at this point.
            i = aux[i-1]