Given a number of airports connections with the time duration between them find the route that pass through all airports in the shortest time possible (returns to the same airport are excluded).
The problem can be translated as: find the Minimum Spaning Tree (MST) in an undirected weighted connected graph.
A MST is a subgraph consisting of all the nodes in the graph with one exclusive path from a node to every other one (no cycles) and having the minimum sum of all edges weight among all such subgraphs.
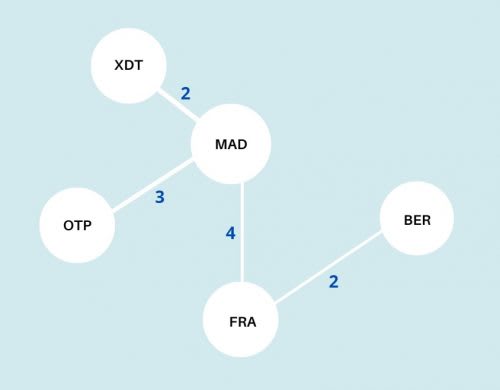
Example of 5 airports with 7 direct flight connections and their duration in hours:
5 7
MAD XDT 2
MAD OTP 3
MAD FRA 4
MAD BER 4
XDT OTP 3
OTP FRA 4
FRA BER 2
The shortest route through all airports would take 11 hours:
MAD -- XDT ( 2 )
FRA -- BER ( 2 )
MAD -- OTP ( 3 )
MAD -- FRA ( 4 )
time: 11
Example of 4 airports with 6 direct flight connections and their duration in hours:
4 6
ANK BCN 3
ANK COS 2
DTM ANK 6
BCN DTM 7
COS BCN 4
COS DTM 5
So, from Ankara (ANK) to Barcelona (BCN) are 3 hours to fly.
The shortest route through all airports would take 12 hours:
ANK -- COS ( 3 )
COS -- BCN ( 4 )
COS -- DTM ( 5 )
time: 12
We can use Kruskal algorithm to find a graph minimum spanning tree. If the number of nodes in a graph is V, then each of its spanning trees should have (V-1) edges and contain no cycles.
Kruskal STEPS:
Initialize an empty edge set T
Sort all graph edges by the ascending order of their weight values
Foreach edge in the sorted edge list
Check whether it will create a cycle with the edges inside T
If the edge doesn't introduce any cycles, add it into T
If T has (V-1) edges, exit the loop
return T
The Node.js implementation:
'use strict';
let fs = require('fs'),
readline = require('readline');
class Edge {
constructor(v1, v2, w = 0) {
this.v1 = v1;
this.v2 = v2;
this.w = w;
}
}
class Graph {
constructor(v, e) {
this.v = v;
this.e = e;
this.edges = [];
this.nodes = [];
}
addEdge(edge) {
this.edges.push(edge);
if (!this.nodes.includes(edge.v1)) {
this.nodes.push(edge.v1);
}
if (!this.nodes.includes(edge.v2)) {
this.nodes.push(edge.v2);
}
}
getEdge(pos) {
return this.edges[pos]
}
getEdges() {
return this.edges
}
getNodes() {
return this.nodes
}
// get the root of node
find(subsets, node) {
let nodeInfo = subsets.get(node);
if (nodeInfo.parent != node) {
nodeInfo.parent = this.find(subsets, nodeInfo.parent)
}
return nodeInfo.parent;
}
// unite the x and y subsets based on rank
union(subsets, x, y) {
let xroot = this.find(subsets, x);
let yroot = this.find(subsets, y);
if (subsets.get(xroot).rank < subsets.get(yroot).rank) {
subsets.get(xroot).parent = yroot;
} else if (subsets.get(xroot).rank > subsets.get(yroot).rank) {
subsets.get(yroot).parent = xroot;
} else {
subsets.get(yroot).parent = xroot;
subsets.get(xroot).rank++;
}
}
}
function kruskal(gNodes, gEdges, gFrom, gTo, gWeight) {
let i = 0, j = 0, cost = 0;
let subsets = new Map(),
result = [];
let graph = new Graph(gNodes, gEdges);
while(i < gEdges) {
graph.addEdge(new Edge(gFrom[i], gTo[i], gWeight[i]));
i++;
}
graph.getEdges().sort((edge1, edge2) => {
if (edge1.w === edge2.w) {
return 1;
}
return edge1.w < edge2.w ? -1 : 1;
});
console.log('sorted edges:' , graph.getEdges());
graph.getNodes().forEach(node => {
subsets.set(node, { parent: node, rank: 0 });
});
i = 0;
while(j < gNodes-1) {
let edge = graph.getEdge(i++);
let root1 = graph.find(subsets, edge.v1);
let root2 = graph.find(subsets, edge.v2);
// if the nodes doesn't create a cycle then we add the edge to final subgraph
if (root1 != root2) {
result[j++] = edge;
// update the total weight of the subgraph
cost += edge.w;
graph.union(subsets, root1, root2);
}
}
i = 0;
while(i < j) {
console.log(`${result[i].v1} -- ${result[i].v2} ( ${result[i++].w} )`);
}
console.log('time: ', cost);
}
function readFile(fileName) {
let fileStream = fs.createReadStream(fileName),
rl,
data = '',
index = 0,
gNodes = 0,
gEdges = 0,
gFrom = [],
gTo = [],
gWeight = [];
fileStream.on('error', (err) => {
console.log('file issue: ', err.message)
});
rl = readline.createInterface({
input: fileStream
});
// 'line' event - emitted whenever the input stream receives a new line \n
rl.on('line', (line) => {
data = line.split(' ');
if (index == 0) {
gNodes = parseInt(data[0], 10);
gEdges = parseInt(data[1], 10);
} else if (index <= gEdges) {
gFrom.push(data[0]);
gTo.push(data[1]);
gWeight.push(parseInt(data[2], 10));
}
index++;
});
rl.on('close', () => {
if (gNodes && gEdges && gFrom.length && gTo.length && gWeight.length) {
kruskal(gNodes, gEdges, gFrom, gTo, gWeight);
} else console.log('invalid data file');
});
}
readFile('data1.txt');
Check the code on GitHub
Read more articles like this on Girlsincode



Top comments (1)
This is a wonderful article. I learned a ton for just this article alone.
Thank you :)