Expogo - Google Code Jam

Expogo is a problem from Google Code Jam 2020 - Round 1B

In this article I explore:

• The Problem
• A solution
• Interactive visualization

The Problem

The full statement can be found here at the Code Jam site.

You have just received the best gift ever: an Expogo stick. You can stand on it and use it to make increasingly large jumps.

A few facts from the problem statement:

• You'll use the Expogo in an infinite two-dimensional plane
• You start at point P = (0, 0)
• Your goal is to reach point P = (X, Y)
• All coordinates are integers
• Land exactly at P = (X, Y), in as few jumps as possible
• For the i-th jump, the Expogo moves you 2 ^{i - 1}
  • First jump moves you 1 unit
  • Second jump moves you 2 units
  • Third moves you 4 units, etc...
• You can aim the Expogo in any cardinal direction: North, South, East, or West
• If it is impossible to land at P = (X, Y), say it so by answering IMPOSSIBLE
• Otherwise, answer with a string of cardinal directions ordered from first to last jump

For example, to arrive at P = (2, 3), you'd do South, East, North, then the answer is SEN . Contrary, arriving at P = (-1, -1) is IMPOSSIBLE.

A solution

This solution uses coordinate transformations

Interestingly, the set of possible Expogo jumping lengths, has only one odd number, that is, 1.

• Taking either North or South, first, makes the end Y coordinate odd, and the end X coordinate will be even.
• Taking either West or East, first, makes the end X coordinate odd, and the end Y coordinate will be odd.

That means that jumping with the Expogo any number of times, ends up with an odd coordinate and an even coordinate.

• We can't have both even coordinates X, Y
• We can't have both odd coordinates X, Y

Immediately conclude that jumping to, for example, (R, R) or (R, -R) is impossible.

A quick way to see if a point P is made up of at both even and odd coordinates it to just add the components and check that the result is NOT even:

const isCoordinateOdd = ({ x, y }) => (x + y) % 2 !== 0;

Remember that odd + even = odd, odd + odd = even, and of course, even + even = even

Let's explore the possibilities now. From any given point P = (X, Y), there's is a set of four points where the Expogo can land us, call this set Q.

const Q = [
    [x + Math.pow(2, i - 1), y], 
    [x - Math.pow(2, i - 1), y], 
    [x, y + Math.pow(2, i - 1)],
    [x, y - Math.pow(2, i - 1)]
];

We can always move the coordinates origin to P, and have:

const Q = [
    [Math.pow(2, i - 1), 0], 
    [-Math.pow(2, i - 1), 0], 
    [0, Math.pow(2, i - 1)],
    [0, -Math.pow(2, i - 1)]
];

As we can see, after the first jump, if we keep moving the origin to the landing place after every jump, then the set of Q points where can land next, is always an even distance away.

Hypothesis

We can scale the coordinate system by dividing the coordinates by 2, but in order to do this, we need to make sure that the target coordinate is (even, even).

For example:

• To arrive at P = (2, 3), from (0, 0), lets first jump one unit North, then we are at (0, 1).

• Make (0, 1) the new origin, then P = (2, 2) from this new origin

• Scale the coordinate system by half, then P = (1, 1)

• In this new coordinate system, the Expogo moves again 1 unit!

• In this new coordinate system, we are back at (0,0)

• Move either, East to (1, 0)

• Make (1, 0) the new origin, then P = (0, 1)

• Scaling the coordinate system by half is not impossible because 1 is odd

• Conclude that this path does not land at P = (2, 3), but rather it leads to P = (2, 1).

In step 1, when we moved the origin to (0, 1), P became (2, 2). We should have concluded immediately that such a move is not good, because in the scaled coordinate system, (1, 1) is impossible to reach.

In fact, any P where the X = Y, even, is already a bad option, no need to do the scale step.

Let's refine the hypothesis:

After moving the origin, we can scale the coordinate system by dividing the coordinates by 2, but in order to do this, we need to make sure that the new target coordinate is (even, even), and that after scaling, the coordinate satisfies X + Y = odd number.

Let's try to arrive at P = (2, 3) again:

• From (0, 0) there's four moves, of one unit, we must move North or South because the odd coordinate, 3, lies in the Y axis
• Try to jump North and move the coordinate system origin to (0, 1)
• Scale by half, P = (1, 1), impossible
• Try to jump South and move the coordinate system origin to (0, -1), then P = (2, 4)
• Scale by half, makes P = (1, 2), possible path
• Try to jump East one unit, and move the coordinate system origin to (0, 1), then P = (0, 2)
• Scale by half, makes P = (0, 1), possible path
• Try to jump North, one unit, and we've reached P.
• Then the answer is SEN

The strategy to follow then is:

• Check if the target P has become (0 , 0)
• If not, check if P is odd coordinate
• if so, move towards the odd coordinate of P
• Transform the coordinate system, accumulating the steps taken
• Repeat

With JavaScript, we can write moveExpogo which does this recursively.

const moveExpogo = ({ x, y, steps = "" }) => {
  if (x === 0 && y === 0) {
    return steps;
  }

  const isOddCoordinate = isCoordinateOdd({ x, y });

  if (!isOddCoordinate) {
    return IMPOSSIBLE;
  }

  const { step, nextX, nextY } = moveTowardsOdd({ x, y });
  return moveExpogo({ x: nextX, y: nextY, steps: `${steps}${step}` });
};

Let's write the moveTowardsOdd function, where the magic happens.

const scale = n => n / 2;
function moveTowardsOdd({ x, y }) {
  if (x === 1 && y === 0) {
    // can be finished in one move by moving EAST
    return { step: EAST, nextX: scale(x - 1), nextY: y };
  }

  if (x === -1 && y === 0) {
    // can be finished in one move by moving WEST
    return { step: WEST, nextX: scale(x + 1), nextY: y };
  }

  if (x === 0 && y === 1) {
    // can be finished in one move by moving NORTH
    return { step: NORTH, nextX: x, nextY: scale(y - 1) };
  }

  if (x === 0 && y === -1) {
    // can be finished in one move by moving SOUTH
    return { step: SOUTH, nextX: x, nextY: scale(y + 1) };
  }

  if (x % 2 !== 0) {
    // move EAST
    const wouldBeOdd = isCoordinateOdd({ x: scale(x - 1), y: scale(y) });
    if (wouldBeOdd) {
      return { step: EAST, nextX: scale(x - 1), nextY: scale(y) };
    }
    // better to move WEST
    return { step: WEST, nextX: scale(x + 1), nextY: scale(y) };
  }

  if (y % 2 !== 0) {
    // move NORTH
    const wouldBeOdd = isCoordinateOdd({ x: scale(x), y: scale(y - 1) });
    if (wouldBeOdd) {
      return { step: NORTH, nextX: scale(x), nextY: scale(y - 1) };
    }
    // better to move SOUTH
    return { step: SOUTH, nextX: scale(x), nextY: scale(y + 1) };
  }
}

Since moveTowardsOdd is called by moveExpogo only if the coordinate is odd, then we can conclude that the if branches cover all possible cases.

Remember, odd coordinates (X, Y) in this context are, those where X + Y = odd

The properties nextX and nextY represent P when the origin is moved to a new position.

• Check if the P coordinate is odd, if not, conclude the whole job is IMPOSSIBLE.
• If so move towards the odd coordinate
• Check if there's such a move that ends the jump sequence
• In either case, move the origin to the landing point,
• and scale the coordinate system by half
• Repeat until you arrive at the target P

These two functions solve the problem, for all test sets of Code Jam, even when the coordinates get pretty large.

Test set 3 (Visible Verdict)

1 ≤ T ≤ 100.
-10⁹ ≤ X ≤ 10⁹.
-10⁹ ≤ Y ≤ 10⁹.

• My Code Jam JavaScript implementation, that takes cases from stdin, can be found here.

• A full implementation to run to your hearts desire can be found in this REPL.

Visualization

These type of problems are challenging but also very fun!

Since we've got a string containing the jumping directions at ever i-th step, we can derive the coordinates where the Expogo lands us to reach point P.

JavaScript's array indexing is zero based, so there's no need to subtract one from it when calculating the Expogo jumping distance

const dir2Coords = (directions) =>
  directions.split("").reduce((prev, curr, index) => {
    const [[x, y] = [0, 0]] = prev.slice(-1);
    switch (curr) {
      case NORTH:
        return [...prev, [x, y + Math.pow(2, index)]];
      case SOUTH:
        return [...prev, [x, y - Math.pow(2, index)]];
      case EAST:
        return [...prev, [x + Math.pow(2, index), y]];
      case WEST:
        return [...prev, [x - Math.pow(2, index), y]];
      default:
        throw new Error("Invalid direction");
    }
  }, []);

This REPL does just that! Now we can use any graphical tool to draw the path taken!

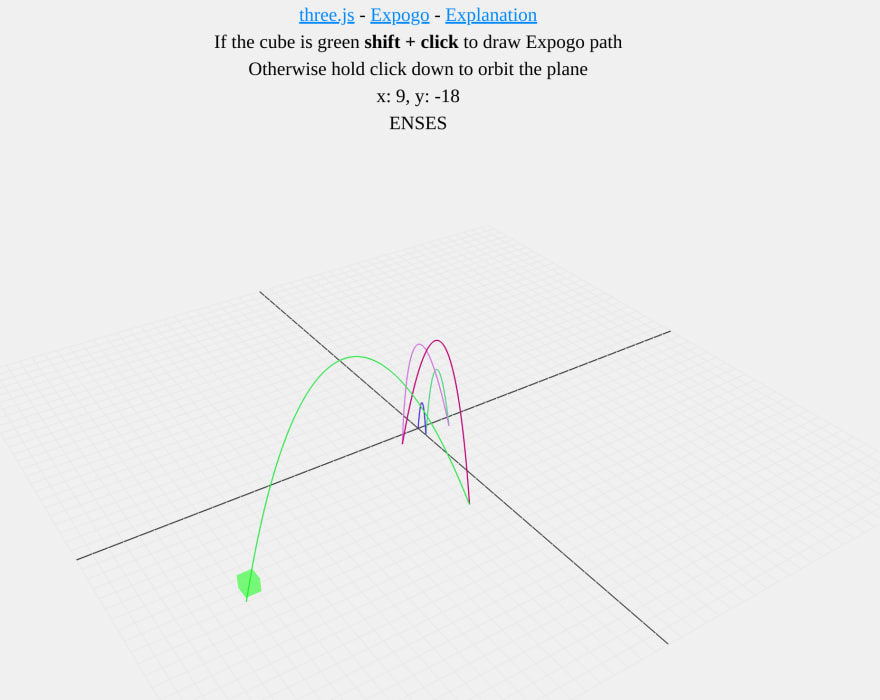
I'll try out three.js for this. In particular the Voxel example, which already makes use of plane and targets coordinates given by the mouse position.

When the user holds down the shift key and clicks on a point, the Expogo path is drawn. Additionally, the mouse is followed by a cube, which is colored red if its impossible for the Expogo to reach it, otherwise it is colored green.

Live version here.

I also try to increase browser support as much as possible by avoiding arrow functions, though this might be futile.

Have you ever tried to compete in Code Jam? I assure you it is very fun!

Happy Hacking!

Comments

[pere]

I gave it a thought to this problem and there's another way to think about it. I'm assuming x and y are always positive... otherwise, flip the offending signs and their corresponding labels (NORTH <-> SOUTH or EAST <-> WEST).

Consider that the binary representation of a coordinate tells you about the jumps you have to do to get it. For example, x = 5 = b101 means that to arrive to x, the 1st and 3rd jumps must go EAST, because 1 + 4 = 5.

So you only have to "follow the bits". If I'm at iteration i, look which coordinate has the i-th bit set to 1, and expend the jump in that axis. The problem is when both x and y need the same jump (both have a 1 in the same position), or when neither of both needs it (both have 0s). In either case the problem is that you don't know where to expend the current jump.

This is solved by fixing the conflict beforehand. In your example of (x, y) = (2, 3) = (b010, b011), you had a conflict in the second jump. What your algorithm have done in the first iteration is, instead of moving NORTH (lowest bit set to 1 in y), you moved SOUTH, changing your distances to (2, 4) = (b010, b100), which has no conflicts from the second jump forwards (and then you yield NORTH and then EAST by just following the bits).

Your strategy of diving by 2 to "transform the coordinate system" is basically doing a right-shift of the bits: you put as "lowest bit" the next thing to do. It's your way of consuming the jumps you have already done; and your parity checking of "will going NORTH create an impossible situation?" is basically saying: is there a conflict at the next jump if I just follow the bits blindly?

When you "follow the bit blindly", you are effectively sustracting 2^i to the distance, which represent you are getting closer (and the i-th bit will flip to 0). But if you do the opposite, moving further away by adding 2^i to the distance, its binary interpretation is that you are flipping that bit to 0, but also toggling all the 1s that follows until the next 0. E.g, bxxx011111111111111111 + 1 = bxxx10000000000000000.

That means that if z is the number whose i-th bit is 1, and the (i+1)-th bit of both numbers are equal (there's a lookahead conflict), adding 2^i to z will flip its (i+1)-th bit breaking the equality and fixing the conflict. The extra 1 that is added in the future position is the extra gargantuan jump that will recover the distance of all of those intermediate jumps, required to sum up to the final number, that you are no longer executing.

The only position at which solving the conflict is not possible is at the first iteration: if x and y are both odd or even, you have a conflict in the first position with no previous jump to fix it.

So, if x and y have the same parity, yield IMPOSSIBLE; otherwise, there's always a solution and the algorithm is (use x and y as distances that you reduce as you get closer to the target):

• At iteration i, find z, e.g., the distance with its i-th lowest bit set to 1.
• If there's no conflict at position i+1, then sustract 2^i to z (reduce the distance).
• Otherwise, add 2^i to z (e.g., increase the distance to break the conflict).
• If you arrived to the target (if x = y = 0), stop; otherwise, ++i and repeat.