After a few surprise encounters with binary trees last week, I thought it'd be good for me to finally get more familiar with them so that later I can tackle binary tree problems with more confidence and less angst.
This is simply an introduction to trees and the different parts that make up the structure. I also touch on what various binary tree structures can look like and why trees, especially binary trees, are applicable and useful.
What are Binary Trees?
Behold, a perfect specimen of the tree data structure in its natural habitat, shot by Marty Kugler
A tree is a data structure that looks like an upside-down tree consisting of nodes. A binary tree is a structure of nodes that each point to no more than two children.
The Physiology of a Tree
A tree is a structure composed of nodes that each contains a value or data. The root is a single node located at the top of the tree. It is the start of the tree where nodes point to child nodes connected by branchlets called edges. A subtree, much like a clipping, is a subsection or part of a tree.
The root of this tree is the parent of two child nodes, each either a left or a right child. Two children or sub-trees of a shared parent are siblings. It's possible for a child to also be the parent of two other child nodes further down the branch.
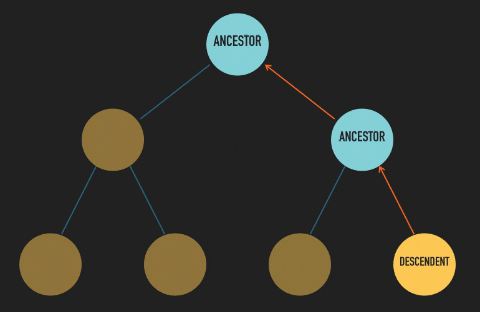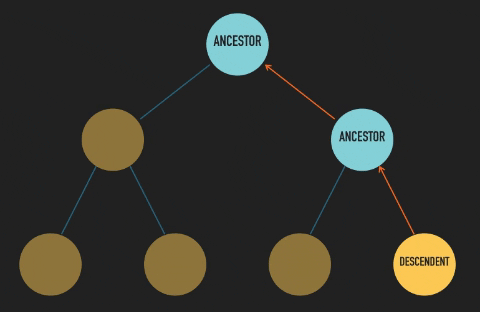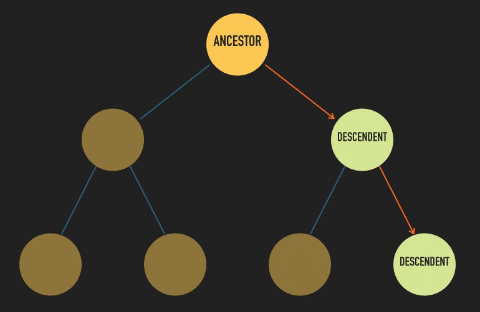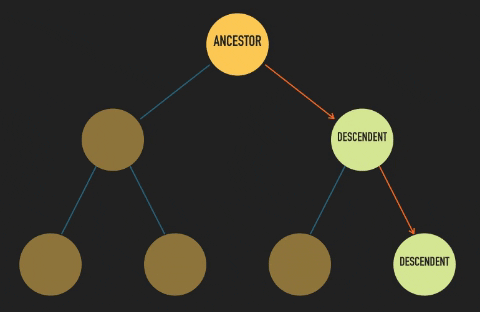
As we follow a branch down from a parent node, any other node located down that branch is its descendent. And if we follow a branch upwards from a child node, any node up that branch is an ancestor of the child node.
At the bottom or terminal of a branch is the leaf or external node, which has no children. Nodes that branch further to one or more child nodes are branch or internal nodes.
Describing a Binary Tree
When we describe a binary tree, we can discuss its height or its depth.
When we talk about a node's depth, we're specifying how many branches or levels down a node is from the root.
However, when we talk about height, we can either describe the height of a node or the height of the tree. In both cases, we're describing the distance from an external node to the node or root.
Binary Tree Identification
Binary trees can be structured differently and possess different kinds of characteristics or qualities.
A full or strictly binary tree is structured so that every node possesses either two or no children.
A complete binary tree is a tree where nodes at every level but the last is required to have two children. On the last level, the children are positioned as far to the left as possible. So, complete binary tree nodes are connected from top to bottom, left to right.
A perfect binary tree is both full and complete. All the leaf nodes are located at the same depth, and all internal nodes have two children.
A balanced binary tree describes a tree where two sibling subtrees don't differ in height by more than one level. If the difference in height is greater than that, then it is unbalanced.
If every node in a tree has only one child, the structure is a degenerate or pathological tree, and is essentially a linked list.
Why are Binary Trees Useful?
Like the family trees many of us are familiar with, trees are hierarchical and can represent structural relationships in the data. More technological examples and applications of trees can be the DOM or your file directory.
Binary Search Trees (BSTs) are especially useful in algorithms because they are naturally sorted, which makes search, insertion, and deletion of values especially quick and efficient. This is definitely worth diving into in another blog post!
For more information on binary trees, check out these other blogs from my 5-part binary tree series!














Top comments (1)
Super informative and easy to follow, thanks Jenny!