Complexity Analysis of Algorithms
Big-O notation (the letter, not the number), also referred to as the order of the function is a big deal when determining how to create a solution to solve a programming problem. It helps us to understand the approximate trade offs or costs of running a particular algorithm.
Big-O notation is used to classify an algorithm by the time it takes to execute that solution and how much space in memory is required in order to do so. As the algorithm grows the run time has potential to as well. Considering the time and space a solution takes will help to provide a great experience for users, teammates, and your future-self. Also, your present self because problem solving is fun!
An algorithm (the code) is the process software engineers implement or tell the computer to solve a particular problem. When determining complexity it is not the time to be optimistic. For efficient algorithms always consider the worst case scenario for the problem and code accordingly.
Case Analysis
The case or scenario can be thought of as the interaction of the user with the algorithm from the interface. In programming the worst-case is actually the best choice. Identifying what could go wrong will decrease the opportunities to have the code fall apart. Minimize the risk. Maximize the optimization. Which means a decrease in time spent re-writing or debugging code. Understanding the best course of action for the worst case scenario goes beyond the size of the problem.
// in this list we need to find a value
const arr = [1, 2, 3, 5, 6, 7, 8, 9, 10, 11, 25, 50];
// uncomment to test
// let case = 1; // best-case returns 0
// let case = 7; // avg-case returns 5
// let case = 50; // worst-case returns ll
for(let i = 0; i < arr.length; i++){
if(arr[i] === case){
return i;
}
}
Because the value is found in the first iteration it is a best-case. There is no need to iterate through the entire array. Great, but what if the value isn't the first but close to the center? This would be the average-case. The iteration stops near the center of the array and returns a value increasing the number of steps required. Lastly, worst-case is when the search ends without finding the value or the value is closer to the last index.
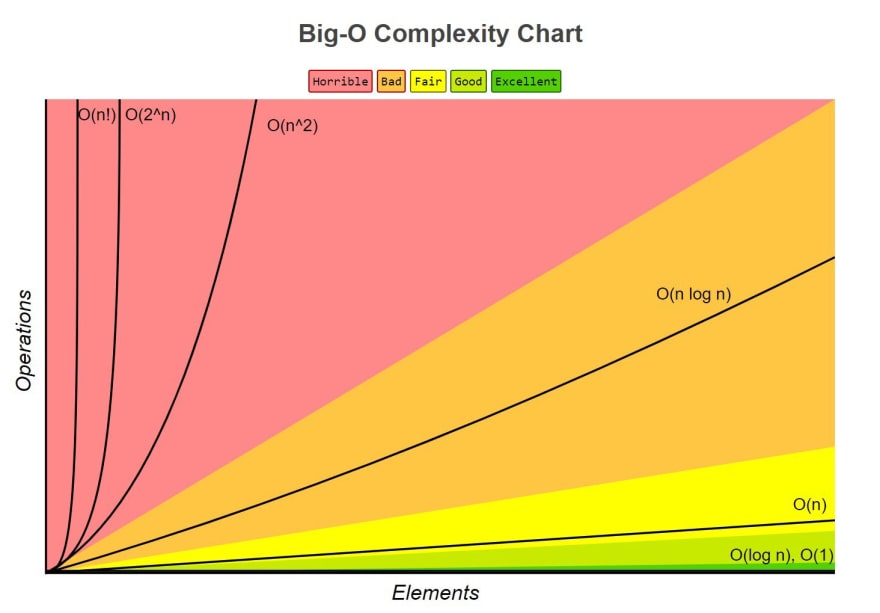
Time Complexity In Order Fastest to Slowest
Here we will cover some trade-offs to consider when choosing an execution method based on what needs to be accomplished.
1. Constant Time Complexity: O(1)
It's fast and it stays the same. This will be any algorithm where the size of the input will not have an effect on the time it takes to execute. It is constant. Only one step is required.
Examples:
Arrays access, Stack, Queue, and Linked List insertion and deletion
//a function that returns the value at the given index of the array in a message
const constantFunFunc = array, index => `Hi, I'm ${array[index]}!`;
console.log(constantFunFunc(['Rod', 'Tina', 'Jessica', 'Jojo'], 3)); //returns "Hi, I'm Jojo!"
Logarithmic Time Complexity: O(log n)
Reduces the size of the input at a decreasing rate. The runtime of a logarithmic algorithm initially increases but only grows in relation to how many choices are left after narrowing down the values to look through. It can be thought of as the opposite of the Quadratic time complexity.
Examples:
Binary Search Tree
// array to be searched by the value
const array = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 25, 50];
const bSearch = (collection, target) => {
// set a start to the zeroth index
let start = 0;
// set end to the last index the array
let end = collection.length -1;
// iterate through the indices
while(start <= end){
// set the middle index
let middle = Math.floor((start + end) / 2);
// if value at the middle index is target return true
if(collection[middle] === target){
return true;
// if the value is less than the target re-assign start the the middle +1
} else if(collection[middle] < target){
start = middle + 1;
} else {
// value is greater than the target re-assign end the middle -1
end = middle - 1;
}
}
// if the value is not in the given collection return false
return false;
}
console.log(bSearch(array, 25)); //returns true
Linear Time Complexity: O(n)
An algorithm whose growth is directly affected by the size of the input data. The iteration stopping early in the execution would be considered a best-case scenario. The execution time would reduce in that situation but there is potentially the need to be able to access any and all information contained within our data.
Examples:
Array iteration
// create a function that takes an array
const iterator = (arr, target)=>{
//loop through the array and push the value into a new array if it is equal to the target
let yourArray = [];
for(let i = 0; i < arr.length; i++){
if(arr[i] === target){
yourArray.push(arr[i]);
}
}
// return the new array
return yourArray;
}
const myArray = ['504424.14', '223141.21'];
console.log(iterator(myArray, '504424.14')) //return ['504424.14']
Quadratic Time Complexity: O(n^2)
As the number of elements grows the execution time grows as well. The execution of one algorithm that is lower on the Big-O scale within another one has the potential to be considered quadratic.
Examples:
Bubble Sort, Nested for loops
const eats = [['hummus', 'smoothie'], ['crawfish', 'snowball'], ['fries', 'pizza'], ['Neyow's','gumbo']];
//find the first letter in the array of nested arrays
//iterated through the array
for(let i = 0; i < eats.length; i++){
//iterate through the array at the index of the outer array
for(let j = 0; j < eats[i].length; j++){
// log the first letter in each
console.log([`${eats[i][j][0]} or ${eats[i][j][1]}`]);
}
} // returns ['h or s']; ['c or s']; ['f or p']; ['N or g']
Conclusion
Some other time complexities are: Exponential Time O(2^n) when the rate of growth doubles as the input increases. Factorial Time O(n!) when the rate of growth is determined by the number of integers from 0 to n. If you would like a brain teaser see Bogosort.
Thank you for reading. I appreciate your time. Happy Coding and remember efficiency is key!

credits:
https://en.wikipedia.org/wiki/Time_complexity#Table_of_common_time_complexities
https://en.wikipedia.org/wiki/Bogosort
https://www.bigocheatsheet.com/
https://www.jenniferbland.com/time-complexity-analysis-in-javascript/
https://en.wikipedia.org/wiki/Big_O_notation




Top comments (0)