This post is the first of a series adapted from my conference talk, Fun, Friendly Computer Science.
I am a terrible cook. Actually, that’s probably not true, I just really dislike cooking so never put any effort into it. But if you’re not like me and you enjoy being in the kitchen, you may be skilled enough to cook with ratios instead of recipes.
Cooking with ratios is when you don't memorize recipes but instead memorize the ratios of ingredients. The amount of ingredients you need changes in proportion to how much of the food you want to make. For example, cupcakes follow a 4:3:2:1 ratio. 4 eggs, 3 cups of flour, 2 cups of sugar, and one cup of butter.
So how is big O notation related to cupcakes? Big O notation measures the relative complexity of a function or algorithm. It measures the complexity in proportion to the size of the function’s input.
Most often complexity refers to running time but it could also be used to measure memory consumption, stack depth, and other resources. We’re going to focus on running time since in a coding interview that’s what they’re usually asking about. And because we’re talking about relative complexity, the actual input size is unimportant because we want to measure the proportional complexity of the code. This will become clearer in our examples.
At its core, big O notation is a mathematical representation of complexity. It is a functional notation of this measurement so all “O”s can be represented on a graph, which can be helpful for those more visually or graphically minded.
If visuals aren’t your thing, this post will also have code samples. For this post, the samples are in Javascript and can be found here, but I also have samples in Ruby and Python if you’re more comfortable with either of those languages.
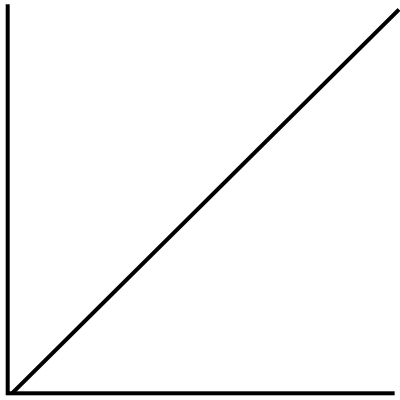
O(1)
The first “O” that you may encounter is O(1) (spoken as O of 1). O(1) is a constant running time. As the input size increases, the time to execute the code remains the same.
An example of this might be if you’re making cupcakes and you need to beat your butter and sugar together for 3 minutes. So regardless of if you’re making a single batch or double batch of cupcakes, it will take 3 minutes to mix together your butter and sugar.
combineButterAndSugar(batches) {
const steps = [];
const butter = {
ingredient: this.recipeRatios.butter,
amount: batches * this.recipeRatios.butter.number
};
const sugar = {
ingredient: this.recipeRatios.sugar,
amount: batches * this.recipeRatios.sugar.number
};
steps.push(this.beatWithMixer([butter, sugar], 3));
steps.push("Combined butter and sugar: O(1)");
return steps.join("<br/>");
}
O(n)
Next up, we have O(n). The running time of the function increases in direct proportion to the input size. In other words, as the input size increases the time to execute increases linearly.
A single for loop or while loop is a great indicator that a function is O(n). For example, when adding eggs to our cupcake batter, we need to add 1 egg at a time and then beat the batter with an electric mixer for 1 minute. So if we need 4 eggs per batch of cupcakes, it would look like 1) add an egg, beat for a minute, 2) add an egg, beat for a minute, 3) add an egg, beat for a minute, 4) add an egg, beat for a minute. You may notice that this running time is actually 4n but with big O notation, coefficients are unimportant. Again, we’re measuring relative complexity and degrees of complexity in terms of n are specific enough, we don’t need to increase specificity with the coefficients.
addEggs(batches) {
const steps = [];
const oneEgg = { ingredient: this.recipeRatios.eggs, amount: 1 };
const butterMixture = { ingredient: "butter mixture" };
const amount = batches * this.recipeRatios.eggs.number;
for (let egg = 0; egg < amount; egg++) {
steps.push(this.beatWithMixer([oneEgg, butterMixture], 1));
}
steps.push("Added eggs: O(n)");
return steps.join("<br/>");
}
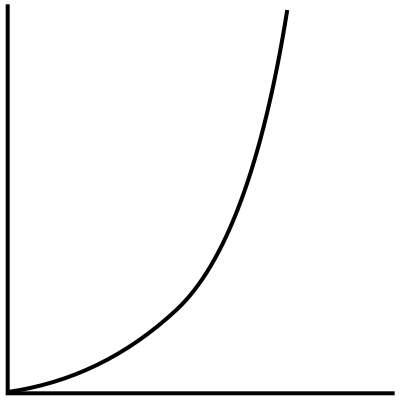
O(n^2)
Our next “O” is getting a little less performant. O(n^2) means that the running time increases in proportion to the square of the input size.
Increasing in proportion to the square of the input size may seem uncommon, but it's actually very common. Any time you see nested loops, you are most likely dealing with O(n^2) or its siblings. As you increase the depth of the nested loops, the exponent increases. So loops nested to 2 levels deep are O(n^2), 3 levels deep are O(n^3), 4 levels deep are O(n^4) and so on and so forth.
combineFlourMixtureAndMilkAndButterMixture(batches) {
const steps = [];
const butterMixture = { ingredient: "butter mixture" };
const flourMixture = { ingredient: "flour mixture" };
const milk = {
ingredient: this.recipeRatios.milk,
amount:
(batches * this.recipeRatios.milk.number) / (batches * batches)
};
steps.push(this.beatWithMixer([butterMixture, flourMixture], 1));
for (let batch = 0; batch < batches; batch++) {
for (let portion = 0; portion < batches; portion++) {
steps.push(this.beatWithMixer([butterMixture, milk], 1));
steps.push(this.beatWithMixer([butterMixture, flourMixture], 1));
}
}
steps.push("Slowly combined milk, flour mixture, and butter mixture: O(n^2)");
return steps.join("<br/>");
}
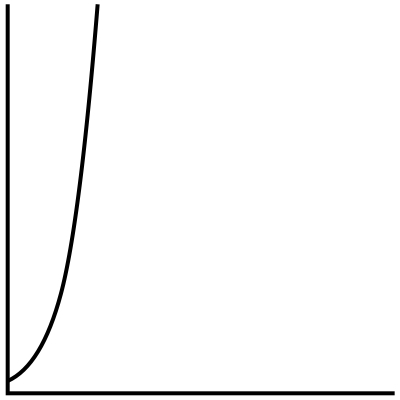
O(2^n)
When the time to execute code grows exponentially with the size of the input, you’re looking at O(2^n). This means that very small increases in input size result in very large increases in running time.
Calculating Fibonacci numbers recursively is an example of an O(2^n) algorithm. If we were throwing a birthday party for Fibonacci and wanted to frost Fibonacci numbers on our cupcakes, we would be looking at exponential running time as we frosted more and more cupcakes. (We’ll be covering recursion soon so don’t worry if that’s new to you.)
fibonacciFrosting(batches) {
const numberToFrost = this.calculateFibonacciNumber(batches);
return `Iced the fibonacci number ${numberToFrost} to all of the cupcakes: O(2^n)`;
}
calculateFibonacciNumber(number) {
if (number <= 1) {
console.log("Fibonacci base case!");
return number;
}
return this.calculateFibonacciNumber(number - 1) + this.calculateFibonacciNumber(number - 2);
}
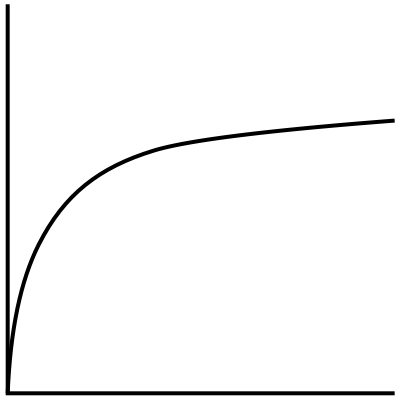
O(log n)
Finally, we have logarithmic running time. I think of O(log n) as the inverse of O(2^n). Where exponential growth sees larger and larger increases in running time as the input size grows, logarithmic growth sees smaller and smaller increases in running time as the input size grows until it approaches a constant running time for large input sizes.
I don’t have a code sample for this since my cupcake metaphor is getting a little stretched 😬, but logarithmic running time is common in divide and conquer algorithms like binary search. If we wanted to hand out our cupcakes using an algorithm with logarithmic running time, we might cut our batch of cupcakes in half and hand to the 2 people nearest to us and ask them to cut their collection of cupcakes in half and hand to the 2 people nearest to them and continue that pattern until everyone has 1 cupcake.
Big O notation uses
Big O notation can be intimidating since it’s very hard to piece together context clues of what it means if you never had the chance to learn it. In the 10 years I’ve been coding, I’ve never used big O notation except in my college CS classes and interviews. So before you interview for a new opportunity, it might be worth refreshing your memory, just in case you have an interviewer who values CS fundamentals over other, more valuable skills (in my opinion).
Big O notation can also be useful for having a shared language to talk about relative code performance with your peers. But don’t feel inadequate if you don’t remember the different “O”s and what they mean. A shared language is nice, but you can also point to nested loops and talk about the negative impact that has on performance without remembering which “O” that is 🤗




Top comments (0)