In my last post, we built a tic-tac-toe bot that would never lose a game! It was great, except it was really slow. It took over 30 seconds to determine the first move.
Lets optimize that using a simple technique to prune the amount of searching we perform for each move!
Our Problem
Why is our bot slow? It’s slow because it’s dumb. There’s no intelligence to how it goes about searching boards.
Lets take the following game board.
It’s X’s turn, what is X going to do? Obviously they’re going to play in the bottom right corner and win.
But our bot sees 5 potential moves X can make, and evaluates each one equally. It eventually picks the bottom right corner as the best move, but not before seeing and comparing all 5 moves against each other. Evaluating all moves equally leads us to do a lot of unnecessary work, which is the main performance problem.
Alpha Beta Pruning – Intuitively
If you recall back to when we discussed our minimax algorithm, one of our players is attempting to maximize the score and the other is attempting to minimize the score. We search the entire tree, alternating taking the max or min at that level to determine the optimal game score.
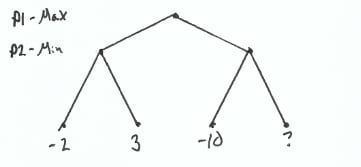
Lets take the following simple tree. Player 1 has the first choice and wants to maximize their score. Player 2 will then take a turn and wants to minimize their score. And notice that our last node doesn’t have a value.
Why doesn’t our last node have a value? It’s empty to demonstrate that the value actually doesn’t matter. We don’t need that node’s value to make the optimal decision.
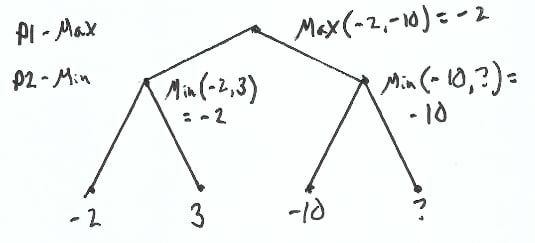
Here’s how we would calculate it.
To calculate the score for the left sub tree, we take the min(-2,3) = -2. So if we go left, we would end up with a score of -2.
Evaluating the one node of the right sub tree, we find a -10. -10 is worse than our left sub tree. We would rather take that -2 score than a -10.
Even though we don’t know every node’s value, we know enough to stop further exploration.
That’s the core idea, stop searching down a particular tree when we are guaranteed to get a worse result than what we already have.
In this example, we saved exploring one node, not a big deal. The benefit comes in avoiding having to search entire subtrees. In more complicated games, such as Chess or Go, with branching factors of ~35 or ~250, anything we can avoid searching is a win!
Alpha Beta Pruning Pseudocode
Now that we’ve discussed the idea behind alpha beta pruning, lets look at the pseudocode.
The algorithm introduces two new variables, called alpha and beta (hence the name of the algorithm), that track each players current state.
- alpha – tracks the lowest score for the maximizing player, initialized to negative infinity.
- beta – tracks the highest score for the minimizing player, initialized to positive infinity.
Lines 12 and 20 hold the potential to stop evaluating whenever it’s useless to. Whenever the lowest score for the maximizing player (alpha) is greater than the highest score for the minimizing player (beta), we stop evaluating.
If we get to the point where we realize, “hey this is worse than what we already know”, we stop searching. When we choose to stop searching down a path, we say that we’re pruning. Hence the name of the algorithm.
Lets take a look at what this looks like in our tic-tac-toe bot.
AbBot – AlphaBeta Bot
Lets start by taking another look at our invincibot.
For every board, we:
- Generate the legal moves (line 27)
- Search down the subtree of each potential move (lines 30-36), keeping track of the value that each subtree has (candidate_choices).
- We only stop whenever someone either wins or the game is tied (lines 19-25)
- Determine the max and min moves (lines 38-41)
- Then return the corresponding move depending on whether the player is looking for max or min (lines 45-48) Point #3 is the important step, we only stop when the game ends. We need a better way to stop searching.
Lets implement alpha beta pruning for our tic tac toe bot now to do that.
You’ll notice it’s a mix of my previous bot code with the alpha beta pseudocode. Notable points are:
- We initialize our alpha and beta to -100 and 100 (line 59), those values are both small/big enough for our needs.
- Lines 40 & 47 hold the potential to stop evaluating early, depending on our alpha and betas.
- The rest is pretty much the same.
How Does It Perform?
If you remember from my last post, the optimal game of tic-tac-toe always ends in a tie. When two players play against each other who always pick the best move, the game ties. It’s only when a player makes a mistake that someone will win.
That’s what happened when we played our invincibot against itself, it tied all day long.
When we pit our abbot against itself and against invincibot, it also ties all day long.
- abbot (x) vs invincibot (o)
- x wins: 0
- o wins: 0
- ties: 15
- invincibot (x) vs abbot(o)
- x wins: 0
- o wins: 0
- ties: 15
- abbot (x) vs abbot(o)
- x wins: 0
- o wins: 0
- ties: 15
So our bot makes the same optimal choices, but what about the number of board states explored? We coded our abbot in order to reduce the searching, which would help it play faster.
Here’s the decrease in boards searched through in invincibot compared to our abbot:
- 1st move: 294,778 => 12,413 => ~95% decrease
- 2nd move: 31,973 => 1,675 => ~95% decrease
- 3rd move: 3,864 => 525 => ~86% decrease
- 4th move: 478 => 44 => ~90% decrease
- 5th move: 104 => 38 => ~63% decrease
- 6th move: 26 => 10
- 7th move: 8 => 6
- 8th move: 3 => 3
- 9th move: 1 => 1
This means that roughly 95% of boards that our original bot search through for the first two moves were redundant. That’s an impressive reduction!
Also when two abbots play against each other, the games only takes about 1 sec. Whereas when two invincibots play against each other, the games takes about 1.5 mins. Another impressive reduction.
Final Thoughts
Implementing alpha-beta pruning drastically improved the performance of our bot. I really enjoyed implementing this and seeing this level of improvement.
I think next week I’ll look into implementing a Monte Carlo type search for our bot. While not necessary to solve tic-tac-toe, this technique is vital in tackling more complicated games.
If you’re interested in learning more about game playing bots and machine learning, follow me on twitter, I’ll be learning, writing and tweeting about it as I do it.
Github repo with code samples.



Top comments (0)