In this post, we will look at Forward mode auto differentiation(auto diff) using Python’s Abstract Syntax Tree(AST).
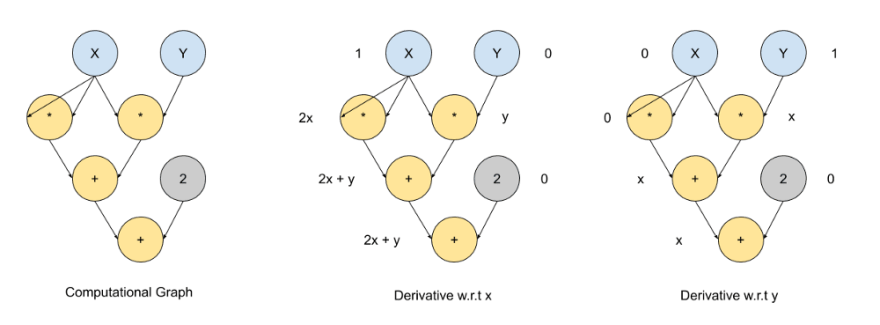
The above image is a typical image of AutoDiff and it is very similar to a typical image of an AST, which essentially breaks down a set of instructions into individual components.
So simply put, the task was to look at a set of math operations and create an equivalent set of differential operations for the math operations. This is possible using Python's ast module. And later on, use the math and differential operations to perform linear regression.
I am assuming you are familiar with AutoDiff and Python AST. We will directly look at using the Python AST to create the AutoDiff forward mode functionality.
So let’s get started.
The Variable Class
We will create a Variable class that will help us keep track of the name of the variable and the value. Tracking the name of the variable is key to generating differential equations. The Variable class also has overloads for the common math operations.
class Variable:
def __init__(self, name: str = '', value: float = 0.0):
self.name = name
self.value = value
# Sample Add overload
def __add__(self, other):
if isinstance(other, self.__class__):
value = self.value + other.value
return Variable(self.name + '_A_' + other.name, value)
else:
value = self.value + other
return Variable(self.name + '_A_' + str(other), value)
We will use objects of this class as our variables.
Predict and Loss Function
Assume the following code, which is common in linear regression.
def train_loop(X, y, w, b):
'''
X - Single Input Feature len(X) == 1
y - Single Output Value
w - Trainable weight parameter
b - Trainable bias parameter
'''
y_pred = w * X + b # Linear equation for prediction
loss = (y_pred - y) ** 2 # MSE with no mean. Because len(X) == 1
return loss
'''
Where
X = Variable(name='X', value=3)
y = Variable(name='y', value=7)
w = Variable(name='w', value=np.random.rand(1))
b = Variable(name='b', value=np.random.rand(1))
'''
We need to find how much w and b should change so that the loss is minimum i.e the value of y_pred is closer to y. This is done through a process called Gradient Descent, in which we get the partial derivatives(Gradients) of the loss function with respect to the trainable parameters w and b.
Python AST
Consider only the first operation y_pred = w * X + b in the above train_loop.
The following is the AST generated by Python for
import ast
print(ast.dump(ast.parse('y_pred = w * X + b'), indent=2))
'''
Module(
body=[
Assign(
targets=[
Name(id='y_pred', ctx=Store())],
value=BinOp(
left=BinOp(
left=Name(id='w', ctx=Load()),
op=Mult(),
right=Name(id='X', ctx=Load())),
op=Add(),
right=Name(id='b', ctx=Load())))],
type_ignores=[])
'''
The value of the Assign node is a Binop operation which again has a Binop as its left input. We separate the "cascading" Binop operations such that each Binop has separate Assign node. This will help in generating the differential equation for that particular Binop. These equations give us the Gradient for each parameter.
Flatten Operation
We pass the above code through a "flattening operation" to extract the individual operations, thereby "flattening" the AST.
# Input to Flattening function
y_pred = w * X + b
# AST is generated from the input.
# AST is parsed and every Binop operation is given its own Assign Node.
# This Assign node is added to the AST to generate new code.
# Output from Flattening function
random_name_1 = w * X
random_name_2 = random_name_1 + b
y_pred = random_name_2
Following in the AST of the above Output
import ast
print(ast.dump(ast.parse(
'''
random_name_1 = w * X
random_name_2 = random_name_1 + b
y_pred = random_name_2
'''), indent=2))
'''
Module(
body=[
Assign(
targets=[
Name(id='random_name_1', ctx=Store())],
value=BinOp(
left=Name(id='w', ctx=Load()),
op=Mult(),
right=Name(id='X', ctx=Load()))),
Assign(
targets=[
Name(id='random_name_2', ctx=Store())],
value=BinOp(
left=Name(id='random_name_1', ctx=Load()),
op=Add(),
right=Name(id='b', ctx=Load()))),
Assign(
targets=[
Name(id='y_pred', ctx=Store())],
value=Name(id='random_name_2', ctx=Load()))],
type_ignores=[])
'''
As you can see we have one Binop operation per Assign node.
Create Differential Equations
We can now generate a differential equation for each operation, with respect to the trainable parameters.
These equations are added to the flattened function which can be then called to get the output of the operation as well as the partial derivatives(gradients) of the output with respect to the parameters.
Putting it together
So putting it all together, when we take the train_loop(X, y, w, b) function from above through the process we get the following output.
# Input Function to Flatten function
def train_loop(X, y, w, b):
y_pred = w * X + b
loss = (y_pred - y) ** 2
return loss
# Output of the Flatten function
def train_loop_flat(X, y, w, b):
w_mult_X = w * X
w_mult_X.name = 'w_mult_X'
w_mult_X_add_b = w_mult_X + b
w_mult_X_add_b.name = 'w_mult_X_add_b'
y_pred = w_mult_X_add_b
y_pred.name = 'y_pred'
y_pred_sub_y = y_pred - y
y_pred_sub_y.name = 'y_pred_sub_y'
y_pred_sub_y_pow_uta = y_pred_sub_y ** 2 # uta is a random id
y_pred_sub_y_pow_uta.name = 'y_pred_sub_y_pow_uta'
loss = y_pred_sub_y_pow_uta
loss.name = 'loss'
return loss
# Output of the Create Differential Equations Function
def train_loop_flat_and_diff(X, y, w, b, dw=0, db=0):
w_mult_X = w * X
w_mult_X.name = 'w_mult_X'
w_mult_X_add_b = w_mult_X + b
w_mult_X_add_b.name = 'w_mult_X_add_b'
y_pred = w_mult_X_add_b
y_pred.name = 'y_pred'
y_pred_sub_y = y_pred - y
y_pred_sub_y.name = 'y_pred_sub_y'
y_pred_sub_y_pow_uta = y_pred_sub_y ** 2
y_pred_sub_y_pow_uta.name = 'y_pred_sub_y_pow_uta'
loss = y_pred_sub_y_pow_uta
loss.name = 'loss'
dw_mult_X = dw * X
dw_mult_X_add_b = dw_mult_X + db
dy_pred = dw_mult_X_add_b
dy_pred_sub_y = dy_pred
dy_pred_sub_y_pow_uta = 2 * y_pred_sub_y ** 1 * dy_pred_sub_y
dloss = dy_pred_sub_y_pow_uta
return (loss, dloss)
The train_loop_flat_and_diff above has inputs dw and db for the trainable parameters w and b respectively. The differential equations are created using the Chain Rule of derivatives.
Linear Regression test
We will now put our forward mode auto diff to the test. We will have an input variable X and an output variable y, along with w and b initialized as follows
def train_loop(X, y, w, b):
y_pred = w * X + b
loss = (y_pred - y) ** 2
return loss
def main():
X = Variable(name='X', value=np.random.rand(1) * -100) # -100.0 : 0.0
y = Variable(name='y', value=np.random.rand(1) * 100) # 0.0 : 100.0
w = fm_ast.Variable(name='w', value=np.random.rand(1))
b = fm_ast.Variable(name='b', value=np.random.rand(1))
epochs = 100
learning_rate = 0.0001
train_losses = []
# ForwardModeAutoDiffAST contains all the functionality described above
# Takes the "training function" and paramter names as inputs
fm_ad = ForwardModeAutoDiffAST(train_loop, [w.name, b.name])
for epoch in range(epochs):
gradients = fm_ad.get_gradients(X=X, y=y, w=w, b=b)
w = w - gradients[w.name][1].value * learning_rate
w.name = 'w'
b = b - gradients[b.name][1].value * learning_rate
b.name = 'b'
train_losses.append(gradients[w.name][0].value)
'''
X=[-95.6548842] y_pred=[-38.00573576], y=[3.70300017]
Train Loss at 0 = [1739.61865285]
Train Loss at 10 = [42.05417673]
Train Loss at 20 = [1.01663303]
Train Loss at 30 = [0.02457646]
Train Loss at 40 = [0.00059412]
Train Loss at 50 = [1.43624806e-05]
Train Loss at 60 = [3.47203852e-07]
Train Loss at 70 = [8.39343273e-09]
Train Loss at 80 = [2.02905909e-10]
Train Loss at 90 = [4.90512154e-12]
X=[-95.6548842] y_pred=[3.70299982], y=[3.70300017]
'''
As seen above the loss has greatly reduced throughout the training and the y_pred and y values are nearly equal at the end.
Following is the uncommented, unoptimized first working version.
Thank you for reading, and hope to post Part 2 soon.



Top comments (0)