If you want to know how Hierarchical Deterministic (HD) wallets work, you're in the right place. We will get down to the fundamentals of cryptography and mathematics to solidify our learning.
To make the most out of this blog, I am assuming you have had some sort of interaction with blockchain in the past. Especially with the process of signing up for a wallet.
So as you may know, each time we sign up for a blockchain wallet, we are presented with a long list of words (sequence-sensitive) that is to be kept a secret. Because if you don't, anyone with this list can withdraw assets from your account.
You can tell if it is an HD Wallet if it presents you with this list of words, formally known as a mnemonic phrase. HD Wallets can potentially have infinite number of account addresses and private keys. Your wallet's UI may choose to present just 10 or 20 of them.
It is important to securely store this mnemonic phrase because this phrase has the ability to regenerate the exact same addresses and their corresponding private keys. And, keep in mind that anybody with this mnemonic phrase or private key will have full control over the entire wallet or the particular address respectively.
In Short...
HD wallets are hierarchically determined from a single seed and you can regenerate the same list of accounts every time using the same mnemonic phrase. The ability to regenerate the same future state using a given set of inputs is called deterministic. Thus, HD wallets are a combination of hierarchical and deterministic.
At this point, you might have some burning questions like: But where do these addresses come from? How does a mnemonic phrase work? Can we pick random words from a dictionary and create our very own mnemonic?
This post will explain the fundamentals of mnemonics by:
- Creating a private key
- Computing a mnemonic seed using a given private key
- Encoding the seed into human-readable mnemonic phrase
I hope that by the end of this article you will understand the nuts and bolts of mnemonic phrases.
“Any sufficiently advanced technology is indistinguishable from magic.” - Arthur C. Clarke
Mnemonic Phrases and Blockchain
The genesis of mnemonics dates back to ancient Greek times. It is a simple memorization technique that encodes and recalls information effectively. In computer science it is both time and memory efficient.
Here’s a well-known mnemonic which helped many of us during elementary math classes; King Henry Died Mother Didn’t Cry Much. This decodes to: Kilometer, Hectometer, Decameter, Meter, Decimeter, Centimeter, and Millimeter. (Yes, the metric system is confusing for some of us.)
Blockchain uses the same technique!
A typical blockchain mnemonic phrase looks like this:
section canal ice eternal city bamboo sunset skill note scare entire couple van ancient absurd window grunt arm runway season found
These words may sound random to an average person, but blockchain wallet software can derive a ton of information from it, like addresses and private keys. This means that your mnemonic phrase is the key to your blockchain accounts. Hence, it is necessary to protect it.
Mnemonic phrases won the confidence of the blockchain community because:
- They make account backup very simple by completely eliminating the need to store private keys
- The same mnemonic phrase can be used in different wallet software provided by different vendors (given that the same standards are used to implement it)
- They enable its users to operate with more freedom. Users can create multiple accounts for diverse purposes. For example, one account for just receiving payments and other one for encrypting files.
Mnemonics in action
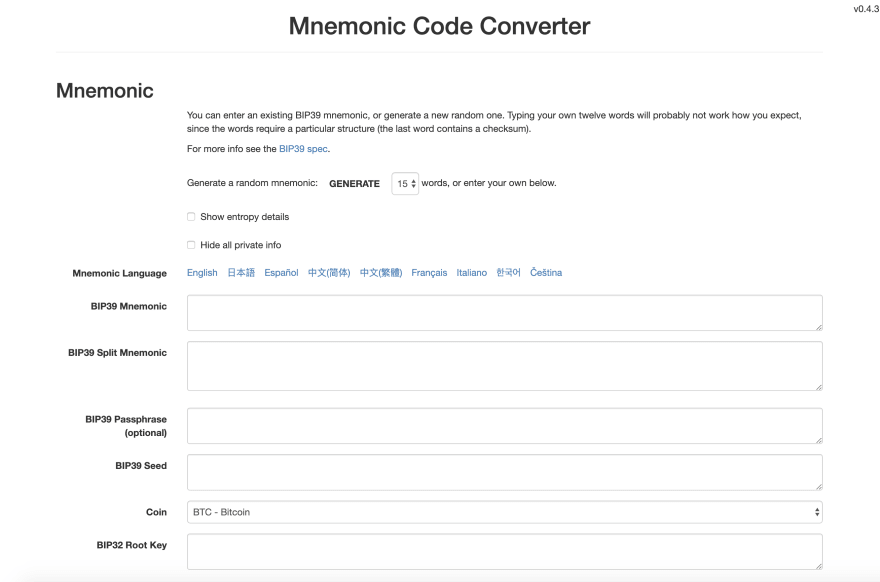
Let’s see the mnemonic magic in action by using one of the most badass tools celebrated by the blockchain community created by Ian Coleman; Mnemonic Code Converter (otherwise known as the BIP39 tool). This tool is most commonly used to derive blockchain addresses using a mnemonic phrase.
⚠️ We highly recommend you to download the tool and use it offline. This tool should not be used online. There are countless number of online scams attempting to steal your mnemonic phrase. ⚠️
To use the Mnemonic Code Converter offline, download the bip39-standalone.html file from here. Open this HTML file in any browser. To stay on the safe side, make sure you are not connected to the internet while using it.
You can either create your mnemonic phrase by clicking on the ‘Generate’ button. You can also define the number of words the mnemonic phrase should have. A longer mnemonic phrase guarantees more security because it has a higher degree of randomness or entropy.
To add an extra layer of security, you can enter a mnemonic passphrase. This passphrase is like a lock on your accounts. In other words, a mnemonic passphrase is used to add Two-Factor Authentication (2FA). To unlock the suite of HD accounts, you need to enter this passphrase. Ultimately, this mnemonic passphrase gets encoded in the resultant mnemonic seed. Therefore, having the protection of a mnemonic passphrase enhances entropy of mnemonic phrase. The same mnemonic with different passphrases will yield different accounts.
The BIP-39 tool can not only be used for Bitcoin but for many other coins. For example ethereum, dogecoin, zcash, etc.
You can select the coin for which you want to generate HD accounts. By default, it is set to Bitcoin. If you change the cointype, the addresses generated will be for the coin you selected. The same mnemonic will generate different addresses for different coins. This is simply because the protocol to generate an address from a private key is different for each coin.
Deriving Addresses
On scrolling down, you will see addresses and their corresponding public-private key pair.
All the addresses and keypairs are generated from a single seed (i.e. the mnemonic phrase). This is the beauty of HD accounts.
All accounts created are hierarchically determined from a single seed and you can regenerate the same list of accounts every time using the same mnemonic phrase.
Scientifically speaking, the ability to regenerate the same future state using a given set of inputs is called deterministic.
Thus, HD accounts are a combination of hierarchical and deterministic.
Now, it’s time to put on our first principle goggles understand this process bottom up
In raw form, a mnemonic is nothing but a randomly chosen large number. This number can be 128 bits, 160 bits, 192 bits, 224 bits, or 256 bits. The word ‘randomly’ is essential here because we do not want to create a predictable mnemonic (as this would lead to poor security).
Now, let’s take an unbiased coin. (When tossing an unbiased coin, the probability of heads showing up is the same as that of tails showing up i.e. 0.5.) The next step is to flip it 128 times. Let’s denote heads with 1 and tails with 0. Ultimately we will end up with a 128-bit binary number which may look like:
10101100 11011100 00111110 10010010 01111001 01000000 10100110 01000101 11000101 00011101 00000101 10011101 11000100 01110110 10100000 11101100
In hexadecimal representation, this number is:
acdc3e927940a645c51d059dc476a0ec
The next step is to apply the SHA256 algorithm on the 128-bit random number. This will give us a 256-bit hash.
a5f1cc6ff28228b130455a7eb05f5367f53c9bce9443393e35cbf5a9f8f9a570
The next step is to find the length of the checksum. A checksum is a sequence of numbers or characters. It is used to check any data for errors that may occur due to transmission or storage.
Length of checksum = mnemonic length (bits) / 32
In our case, the mnemonic length is 128. So, the length of our checksum is 128 / 32 = 4.
Now take the first four bits of the 256-bit long hash (should be equal to the length of the checksum) and append these four bits to the end of the randomly generated 128-bit number i.e. a5f1.
In binary, this number is:
10101100 11011100 00111110 10010010 01111001 01000000 10100110 01000101 11000101 00011101 00000101 10011101 11000100 01110110 101000001 11011001 01001011 1110001
Now, make groups of 11 bits each. You will end up with 12 groups. (The total number of bits is 132) Each group represents a decimal index number of a lookup table. The total number of words in this lookup table is 2^11 (2048) with indices ranging from 0 to 2047. The total number of 12-word mnemonics that can be generated is 2048^12.
This lookup table (formally known as a word-list) can be found here. The order of words should not be changed because each word is hard-linked to an index value.
This word-list exists for English, Japanese, Korean, Spanish, Chinese (Simplified), Chinese (Traditional), French, and Italian.
These words make up a human-readable mnemonic phrase.
So now we know how to create a human-readable mnemonic from a random number.
This algorithm is the BIP-39 standard.
We learned how to:
- Create a completely random private key by flipping a coin
- Compute a mnemonic seed using a given private key
- Encode the seed into human-readable mnemonic phrase
While mnemonic phrases were meant to make complicated cryptography human-readable, a list of 12 random words isn’t exactly intuitive for most users to remember or store.
For mass adoption of blockchain technology, we need to create tools that are not just human-readable, they need to be intuitive. There is little meaning in pursuing Layer 2 solutions and ZKSnarks if there isn’t a dead simple fundamental layer comprised of tools that are easy for everyday people to use and understand.







Top comments (0)