You can sort a large amount data using an external sort. All the sort algorithms discussed in the preceding sections assume that all the data to be sorted are available at one time in internal memory, such as in an array. To sort data stored in an external file, you must first bring the data to the memory and then sort it internally. However, if the file is too large, all the data in the file cannot be brought to memory at one time. This section discusses how to sort data in a large external file. This is called an external sort.
For simplicity, assume that two million int values are stored in a binary file named largedata.dat. This file was created using the program in code below.
A variation of merge sort can be used to sort this file in two phases:
Phase I: Repeatedly bring data from the file to an array, sort the array using an internal sorting algorithm, and output the data from the array to a temporary file. This process is shown in Figure below. Ideally, you want to create a large array, but its maximum size depends on how much memory is allocated to the JVM by the operating system. Assume that the maximum array size is 100,000 int values. In the temporary file, every 100,000 int values are sorted. They are denoted as S1, S2, ... , and Sk, where the last segment, Sk, may contain less than 100000 values.
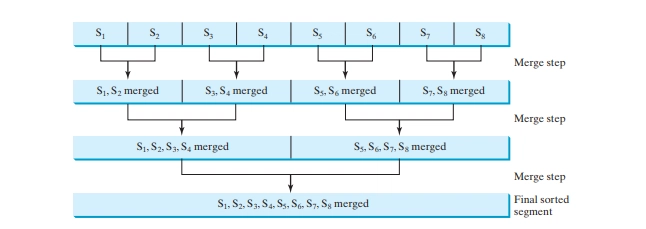
Phase II: Merge a pair of sorted segments (e.g., S1 with S2, S3 with S4, ... , and so on) into a larger sorted segment and save the new segment into a new temporary file. Continue the same process until only one sorted segment results. Figure below shows how to merge eight segments.
It is not necessary to merge two successive segments. For example, you can merge S1 with S5, S2 with S6, S3 with S7 and S4 with S8, in the first merge step. This observation is useful in implementing Phase II efficiently.
Implementing Phase I
The code below gives the method that reads each segment of data from a file, sorts the segment, and stores the sorted segments into a new file. The method returns the number of segments.
1 /** Sort original file into sorted segments */
2 private static int initializeSegments
3 (int segmentSize, String originalFile, String f1)
4 throws Exception {
5 int[] list = new int[segmentSize];
6 DataInputStream input = new DataInputStream(
7 new BufferedInputStream(new FileInputStream(originalFile)));
8 DataOutputStream output = new DataOutputStream(
9 new BufferedOutputStream(new FileOutputStream(f1)));
10
11 int numberOfSegments = 0;
12 while (input.available() > 0) {
13 numberOfSegments++;
14 int i = 0;
15 for ( ; input.available() > 0 && i < segmentSize; i++) {
16 list[i] = input.readInt();
17 }
18
19 // Sort an array list[0..i-1]
20 java.util.Arrays.sort(list, 0, i);
21
22 // Write the array to f1.dat
23 for (int j = 0; j < i; j++) {
24 output.writeInt(list[j]);
25 }
26 }
27
28 input.close();
29 output.close();
30
31 return numberOfSegments;
32 }
The method creates an array with the maximum size in line 5, a data input stream for the original file in line 6, and a data output stream for a temporary file in line 8. Buffered streams are used to improve performance.
Lines 14–17 read a segment of data from the file into the array. Line 20 sorts the array. Lines 23–25 write the data in the array to the temporary file.
The number of segments is returned in line 31. Note that every segment has MAX_ARRAY_SIZE number of elements except the last segment, which may have fewer elements.
Implementing Phase II
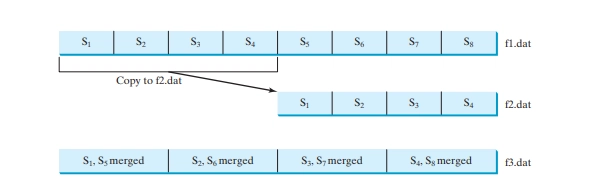
In each merge step, two sorted segments are merged to form a new segment. The size of the new segment is doubled. The number of segments is reduced by half after each merge step. A segment is too large to be brought to an array in memory. To implement a merge step, copy half the number of segments from the file f1.dat to a temporary file f2.dat. Then merge the first remaining segment in f1.dat with the first segment in f2.dat into a temporary file named f3.dat, as shown in Figure below.
f1.dat may have one segment more than f2.dat. If so, move the last segment into f3.dat after the merge.
The code below gives a method that copies the first half of the segments in f1.dat to f2.dat.
1 private static void copyHalfToF2(int numberOfSegments,
2 int segmentSize, DataInputStream f1, DataOutputStream f2)
3 throws Exception {
4 for (int i = 0; i < (numberOfSegments / 2) * segmentSize; i++) {
5 f2.writeInt(f1.readInt());
6 }
7 }
The code below gives a method that merges a pair of segments in f1.dat and f2.dat.
1 private static void mergeSegments(int numberOfSegments,
2 int segmentSize, DataInputStream f1, DataInputStream f2,
3 DataOutputStream f3) throws Exception {
4 for (int i = 0; i < numberOfSegments; i++) {
5 mergeTwoSegments(segmentSize, f1, f2, f3);
6 }
7
8 // If f1 has one extra segment, copy it to f3
9 while (f1.available() > 0) {
10 f3.writeInt(f1.readInt());
11 }
12 }
The code below gives a method that merges two segments.
1 private static void mergeTwoSegments(int segmentSize,
2 DataInputStream f1, DataInputStream f2,
3 DataOutputStream f3) throws Exception {
4 int intFromF1 = f1.readInt();
5 int intFromF2 = f2.readInt();
6 int f1Count = 1;
7 int f2Count = 1;
8
9 while (true) {
10 if (intFromF1 < intFromF2) {
11 f3.writeInt(intFromF1);
12 if (f1.available() == 0 || f1Count++ >= segmentSize) {
13 f3.writeInt(intFromF2);
14 break;
15 }
16 else {
17 intFromF1 = f1.readInt();
18 }
19 }
20 else {
21 f3.writeInt(intFromF2);
22 if (f2.available() == 0 || f2Count++ >= segmentSize) {
23 f3.writeInt(intFromF1);
24 break;
25 }
26 else {
27 intFromF2 = f2.readInt();
28 }
29 }
30 }
31
32 while (f1.available() > 0 && f1Count++ < segmentSize) {
33 f3.writeInt(f1.readInt());
34 }
35
36 while (f2.available() > 0 && f2Count++ < segmentSize) {
37 f3.writeInt(f2.readInt());
38 }
39 }
Combining Two Phases
The code below gives the complete program for sorting int values in largedata.dat and storing the sorted data in sortedfile.dat.
package demo;
import java.io.*;
public class SortLargeFile {
public static final int MAX_ARRAY_SIZE = 100000;
public static final int BUFFER_SIZE = 100000;
public static void main(String[] args) throws Exception {
// Sort largedata.dat to sortedfile.dat
sort("largedata.dat", "sortedfile.dat");
// Display the first 100 numbers in the sorted file
displayFile("sortedfile.dat");
}
/** Sort data in source file into target file */
public static void sort(String sourcefile, String targetfile) throws Exception {
// Implement Phase 1: Create initial segments
int numberOfSegments = initializeSegments(MAX_ARRAY_SIZE, sourcefile, "f1.dat");
// Implement Phase 2: Merge segments recursively
merge(numberOfSegments, MAX_ARRAY_SIZE, "f1.dat", "f2.dat", "f3.dat", targetfile);
}
/** Sort original file into sorted segments */
private static int initializeSegments(int segmentSize, String originalFile, String f1) throws Exception {
int[] list = new int[segmentSize];
DataInputStream input = new DataInputStream(new BufferedInputStream(new FileInputStream(originalFile)));
DataOutputStream output = new DataOutputStream(new BufferedOutputStream(new FileOutputStream(f1)));
int numberOfSegments = 0;
while (input.available() > 0) {
numberOfSegments++;
int i = 0;
for ( ; input.available() > 0 && i < segmentSize; i++) {
list[i] = input.readInt();
}
// Sort an array list[0..i-1]
java.util.Arrays.sort(list, 0, i);
// Write the array to f1.dat
for (int j = 0; j < i; j++) {
output.writeInt(list[j]);
}
}
input.close();
output.close();
return numberOfSegments;
}
private static void merge(int numberOfSegments, int segmentSize, String f1, String f2, String f3, String targetfile) throws Exception {
if (numberOfSegments > 1) {
mergeOneStep(numberOfSegments, segmentSize, f1, f2, f3);
merge((numberOfSegments + 1) / 2, segmentSize * 2, f3, f1, f2, targetfile);
}
else { // Rename f1 as the final sorted file
File sortedFile = new File(targetfile);
if (sortedFile.exists()) sortedFile.delete();
new File(f1).renameTo(sortedFile);
}
}
private static void mergeOneStep(int numberOfSegments, int segmentSize, String f1, String f2, String f3) throws Exception {
DataInputStream f1Input = new DataInputStream(new BufferedInputStream(new FileInputStream(f1), BUFFER_SIZE));
DataOutputStream f2Output = new DataOutputStream(new BufferedOutputStream(new FileOutputStream(f2), BUFFER_SIZE));
// Copy half number of segments from f1.dat to f2.dat
copyHalfToF2(numberOfSegments, segmentSize, f1Input, f2Output);
f2Output.close();
// Merge remaining segments in f1 with segments in f2 into f3
DataInputStream f2Input = new DataInputStream(new BufferedInputStream(new FileInputStream(f2), BUFFER_SIZE));
DataOutputStream f3Output = new DataOutputStream(new BufferedOutputStream(new FileOutputStream(f3), BUFFER_SIZE));
mergeSegments(numberOfSegments / 2, segmentSize, f1Input, f2Input, f3Output);
f1Input.close();
f2Input.close();
f3Output.close();
}
/** Copy first half number of segments from f1.dat to f2.dat */
private static void copyHalfToF2(int numberOfSegments, int segmentSize, DataInputStream f1, DataOutputStream f2) throws Exception {
for (int i = 0; i < (numberOfSegments / 2) * segmentSize; i++) {
f2.writeInt(f1.readInt());
}
}
/** Merge all segments */
private static void mergeSegments(int numberOfSegments, int segmentSize, DataInputStream f1, DataInputStream f2, DataOutputStream f3) throws Exception {
for (int i = 0; i < numberOfSegments; i++) {
mergeTwoSegments(segmentSize, f1, f2, f3);
}
// If f1 has one extra segment, copy it to f3
while (f1.available() > 0) {
f3.writeInt(f1.readInt());
}
}
/** Merges two segments */
private static void mergeTwoSegments(int segmentSize, DataInputStream f1, DataInputStream f2, DataOutputStream f3) throws Exception {
int intFromF1 = f1.readInt();
int intFromF2 = f2.readInt();
int f1Count = 1;
int f2Count = 1;
while (true) {
if (intFromF1 < intFromF2) {
f3.writeInt(intFromF1);
if (f1.available() == 0 || f1Count++ >= segmentSize) {
f3.writeInt(intFromF2);
break;
}
else {
intFromF1 = f1.readInt();
}
}
else {
f3.writeInt(intFromF2);
if (f2.available() == 0 || f2Count++ >= segmentSize) {
f3.writeInt(intFromF1);
break;
}
else {
intFromF2 = f2.readInt();
}
}
}
}
/** Display the first 100 numbers in the specified file */
public static void displayFile(String filename) {
try {
DataInputStream input = new DataInputStream(new FileInputStream(filename));
for (int i = 0; i < 100; i++)
System.out.print(input.readInt() + " ");
input.close();
}
catch (IOException ex) {
ex.printStackTrace();
}
}
}
0 1 1 1 2 2 2 3 3 4 5 6 8 8 9 9 9 10 10 11 . . . (omitted)
Before you run this program, first run the first code in this post, CreateLargeFile.java, to create the file largedata.dat. Invoking sort("largedata.dat", "sortedfile.dat") (line 10) reads data from largedata.dat and writes sorted data to sortedfile.dat. Invoking displayFile("sortedfile.dat") (line 13) displays the first 100 numbers in the specified file. Note that the files are created using binary I/O. You cannot view them using a text editor such as Notepad.
The sort method first creates initial segments from the original array and stores the sorted segments in a new file, f1.dat (lines 19), then produces a sorted file in targetfile(lines 22).
The merge method
merge(int numberOfSegments, int segmentSize, String f1, String f2, String f3, String targetfile)
merges the segments in f1 into f3 using f2 to assist the merge. The merge method is invoked recursively with many merge steps. Each merge step reduces the numberOfSegments by half and doubles the sorted segment size. After the completion of one merge step, the next merge step merges the new segments in f3 to f2 using f1 to assist the merge. The statement to invoke the new merge method is
merge((numberOfSegments + 1) / 2, segmentSize * 2, f3, f1, f2, targetfile);
The numberOfSegments for the next merge step is (numberOfSegments + 1) / 2. For example, if numberOfSegments is 5, numberOfSegments is 3 for the next merge step, because every two segments are merged but one is left unmerged.
The recursive merge method ends when numberOfSegments is 1. In this case, f1 contains sorted data. File f1 is renamed to targetfile (line 62).
External Sort Complexity
In the external sort, the dominating cost is that of I/O. Assume n is the number of elements to be sorted in the file. In Phase I, n number of elements are read from the original file and output to a temporary file. Therefore, the I/O for Phase I is O(n).
In Phase II, before the first merge step, the number of sorted segments is n / c, where c is MAX_ARRAY_SIZE. Each merge step reduces the number of segments by half. Thus, after the first merge step, the number of segments is n / 2c. After the second merge step, the number of segments is n / 2^(2)c, and after the third merge step the number of segments is n / 2^(3)c. After log(n / c) merge steps, the number of segments is reduced to 1. Therefore, the total number of merge steps is log(n / c).
In each merge step, half the number of segments are read from file f1 and then written into a temporary file f2. The remaining segments in f1 are merged with the segments in f2. The number of I/Os in each merge step is O(n). Since the total number of merge steps is log(n / c),
the total number of I/Os is
Therefore, the complexity of the external sort is O(n logn).






Top comments (0)