When we talk about complexity and evaluate algorithm problems, we usually talk about two things:
-
Time Complexity
- Deals with how efficient or fast an algorithm is.
-
Space Complexity
- Deals with how much space or memory it will require.
Complexity is always related to the input, more importantly, the size of the input.
for example:
- O(n): Linear
input= [1,2,3,4,5,6,7,8,9,10]
function countNum(){
let counter = 0
for (let i = 0; i < input.length; i++){
console.log(counter++)
}
}
countNum(input)
//output:
0
1
2
3
4
5
6
7
8
9
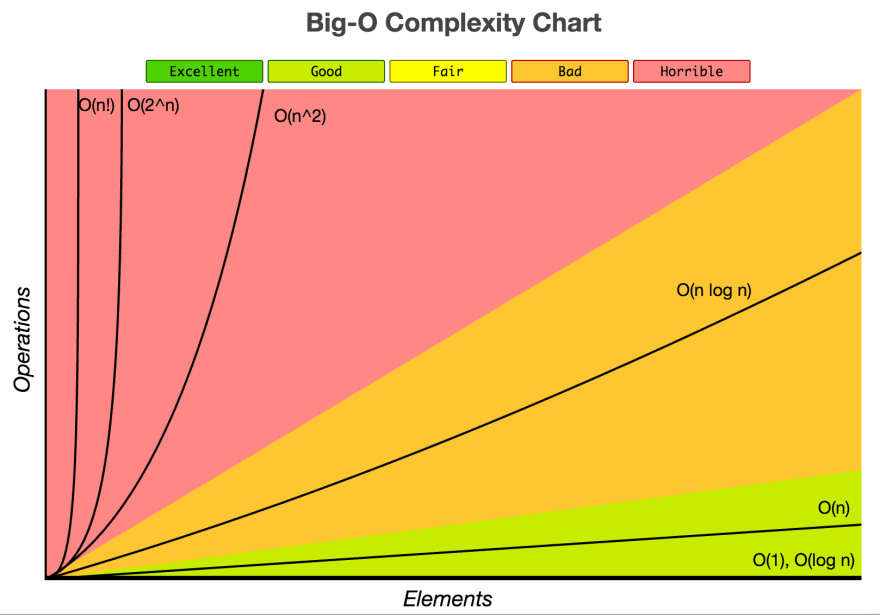
In this example, when we talk about time complexity, we are actually talking about the number of operations. Since the number of input is 10, the number of operations will also be 10. If you increase the number of elements in the array, the number of operations will also increase. It is therefore 1:1 relation. We call this Big O(n), where n is the number of elements in the given array, and since it is 1:1 relation we call this linear.
- O(n^2): Quadratic
input= [1,2,3,4,5,6,7,8,9,10]
function countNum(){
let counter = 0
for (let i = 0; i < input.length; i++){
for(let j = 0; j < input.length; j++){
console.log(counter++)
}
}
}
countNum(input)//
Check the console.log, you will see
the operation has increased by 10folds
In this example, the number of operations is growing faster than the input. We have a nested loop, each loop has a time complexity of O(n), so we multiply the time like so: O(n) * O(n) = O(n^2). Note: We don't really focus on the coefficients, all we care about is the power.
- O(logn) Logarithmic
It is the opposite of exponential growth. For example in binary search the input is sorted and split into two, where one half is discarded depending on the condition and another half is being checked. This saves time complexity and considered the fastest of solving an algorithm problem after O(1).
- O(1) Constant
Accessing the array index and not looking up the value. Just accessing the index directly. Then push and pop in a Stack is also constant. Removing and inserting from a Queue is considered to have O(1) complexity.
Happy Coding 😄


Top comments (0)