Another problem editorial from Codechef September Long Challenge.
PROBLEM STATEMENT:
There are N athletes (numbered 1 through N) in a line. For each valid i, the i-th athlete starts at the position i and his speed is Vi, i.e. for any real number t≥0, the position of the i-th athlete at the time t is i+Vi⋅t.
Unfortunately, one of the athletes is infected with a virus at the time t=0. This virus only spreads from an infected athlete to another whenever their positions are the same at the same time. A newly infected athlete may then infect others as well.
We do not know which athlete is infected initially. Find the size of this set, i.e. the final number of infected people, in the best and worst possible scenario.
LOGIC
Case 1: If the speed of two athletes is the same, they will never meet. So, in that case, we have surety that the virus won't spread amongst them.
Case 2: If the speed of an athlete at position 4 is greater than that of an athlete at position 2, then in that case also, they will never meet.
Case 3: If the speed of an athlete at position 4 is lesser than that of an athlete at position 2, then, in that case, they will meet.
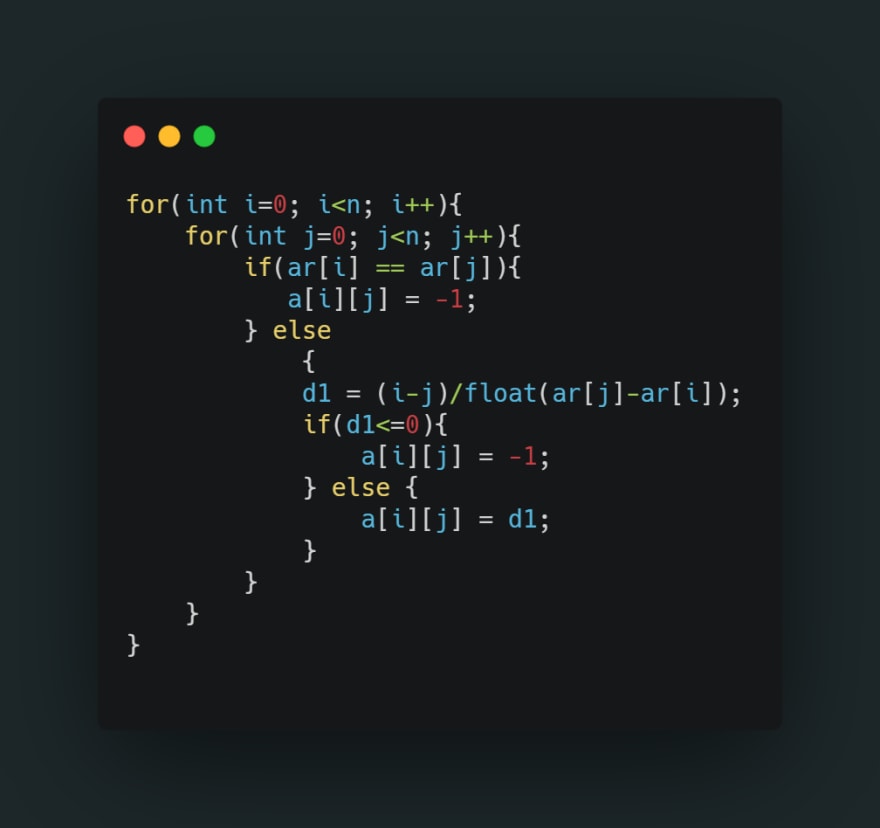
Time Calculation: Time can be calculated by the formula, (pos1 - pos2)/(speed 2 - speed1)
Now, another main point in this question is, one athlete, can only spread COVID19 to another one, only after getting infected. Hence, we can use Depth First Search.
CODE IMPLEMENTATION
Firstly, we will make a 2D vector array and traverse through the given array of athletes and calculate time if they will meet or not, if it is negative, or 0, we will fill -1 in the 2D matrix, else will fill the calculated time.
Now we will use Depth First Search Method in the following manner to find out the maximum and the minimum number of people who can get infected.
Then finally, iterate over that vector v and find out the maximum and minimum element which is the required answer.
That's all, Happy Coding :)





Top comments (0)