Este texto consiste em um pequeno projeto realizado no primeiro semestre de 2020 durante a disciplina de Cálculo numérico na UNICAMP. Aqui vamos avaliar as aplicações do método de mínimos quadrados com dados do tempo médio de viagem entre Terminal Tietê (São Paulo - SP) e o Aeroporto de Guarulhos (sem terminal especificado).
Estes dados foram retirado do Uber Movement, vamos comparar o tempo médio de viagem entre fevereiro e março de 2020 e de 2019.
O caminho escolhido serve para avaliar o fluxo de pessoas, e verificar se no mês de 2020 houve mudanças do trânsito da capital.
Curiosidades: a ideia surgiu depois de vários colegas mudarem de Campinas e eles retornaram para suas cidades natais, alguns amigos moram muito longe e estavam bem com medo da exposição ao COVID-19 devido à grande migração de pessoas no começo da pandemia no Brasil. E verifiquei se no mês de março o trânsito para ir ao Aeroporto de Guarulhos piorou ou não.
Método aplicado
Durante o semestre foi ensinado vários métodos para aproximar vários dados e convertendo em uma função, este problema chamamos o problema do ajuste de curvas, nesta situação, usamos método dos quadrados mínimos [1].
Este método consiste em ler uma tabela de dados com um mapamento de pares (x, y), x corresponde ao dia (de 1/fev até 31/mar) e y ao tempo médio do dia (em segundos).
A partir destes dados, o método MMQ pode criar uma função polinomial phi(x,y) com determinado grau.
Com Python, criei um software que lê estes dados e imprime um gráfico com função phi(x,y) gerada. E estes foram os resultados (arredondados):
- phi_2(x,y)= 130.4 x -2.0 x^2
- phi_3(x,y)= 238.2x - 8.0 x^2 + 0.07 x^3
- phi_4(x,y)=410.4 x -25.2 x^2 + 0.5 x^3 -0.004 x^4
- phi_5(x,y)=616.0 x -5.7 x^2 + 2.2 x^3 -0.04 x^4 + 0.0002 x^5
Ferramentas
Postei o projeto dentro do meu repositório aqui, para quem tiver interesse, usei a IDE do Pycharm, achei bem fácil de usar. Se não quiser usar instalar uma IDE pode usar o Repl.it , como o programa imprime várias imagens pode ser que sua performance seja bem lenta.
Resultados dos gráficos de 2020
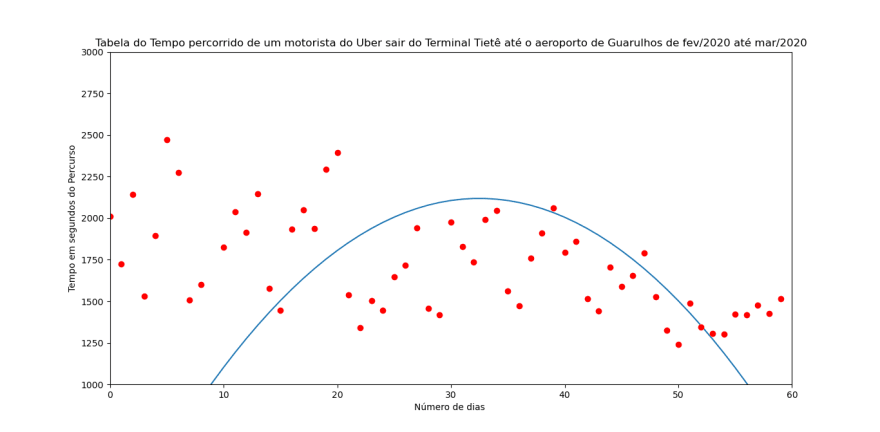
Figura 1: Função de segundo grau

Figura 2: Função de terceiro grau

Figura 3: Função de quarto grau
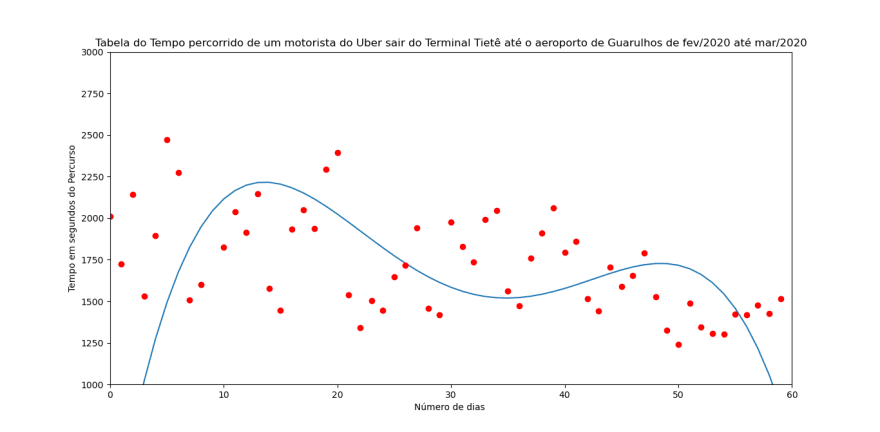
Figura 4: Função de quinto grau
Resultados dos gráficos de 2019
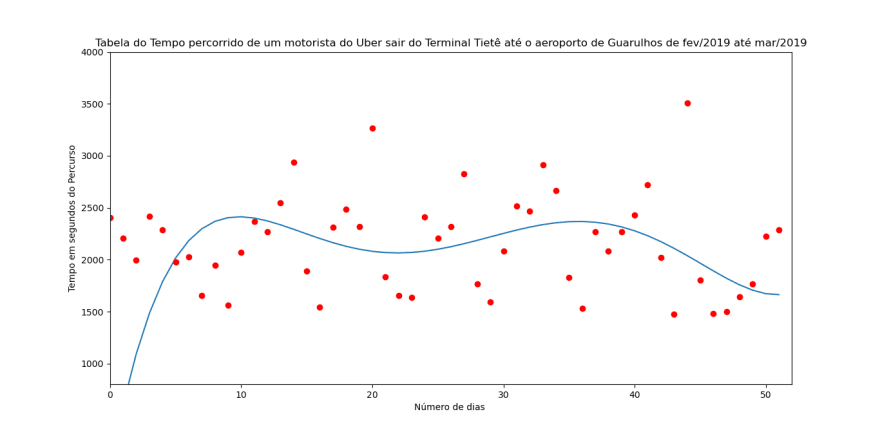
Figura 5: Função de quinto grau com dados de fevereiro e março de 2019
Conclusões
Quando comparamos os dados do tempo médio do gráfico, temos primeiramente, uma pequena falha (que não consegui resolver), de todas as funções começarem do zero. A numeração dos dias segue a ordem de dia 0 é primeiro de fevereiro e dia 60 é 1 de abril.
Durante o mês de fevereiro mostra-se que tem um tempo consistente de 2500 segundos (aproximadamente 41 minutos) de viagem. No entanto, no mês de março mostram-se pequenos sinais da redução do trânsito em São Paulo, e finalmente no final de março, é anunciado o primeiro período de quarentena entre os dias 22 de março até 7 de abril temos uma redução drástica no tempo de viagem, caindo para 1500 segundo (25 minutos).
Este trabalho foi bem interessante e foi muito importante para praticar programação em Python, infelizmente não fiz os estudos de erro e espero que tenham gostado da minha primeira postagem.

Figura 6: Comparação visual entre as funções de quinto grau geradas pelo MMQ em fevereiro e março de 2019 (linha azul) e 2020 (linha laranja)
Referências
[1] RUGGIERO. Márcia A. Gomes, LOPES, Vera Lúcia da Rocha. Cálculo Numérico: Aspectos Teóricos e Computacionais. 2º ed. São Paulo. Pearson
Written with StackEdit.


Top comments (0)