Leetcode#42: Trapping Rain Water

Here in the post I will explain and give solution to Leetcode problem number 42.

42. Trapping Rain Water
Level- hard
Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it can trap after raining.

Example 1:

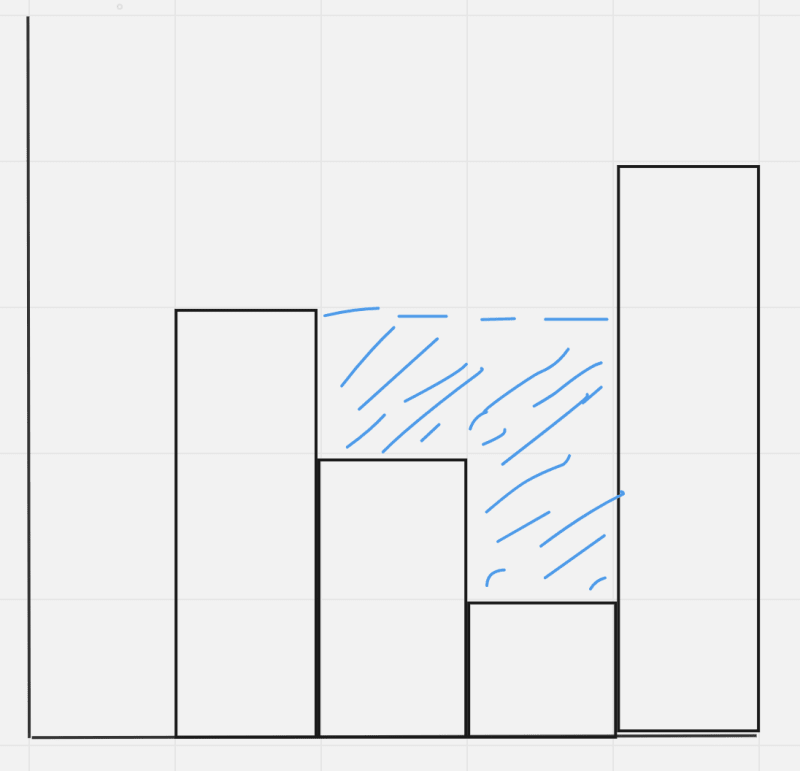
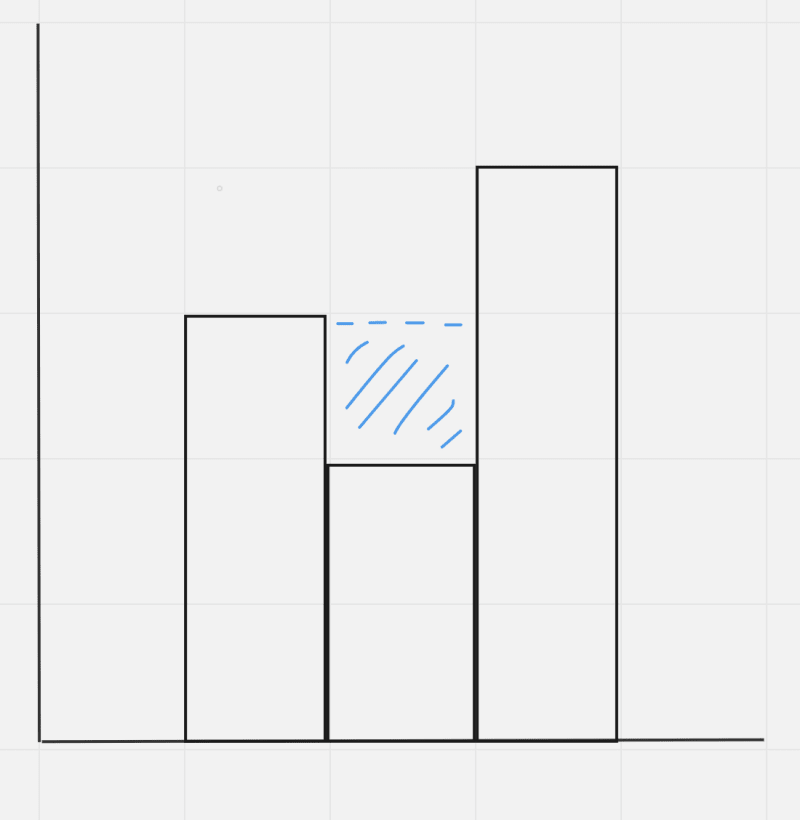
Input: height = [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6
Explanation: The above elevation map (black section) is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.

Example 2:

Input: height = [4,2,0,3,2,5]
Output: 9

Constraints:

n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105

Solution

To reach the solution of this problem, first we need to understand the clues hidden in the question.

Clue 1: Count of tower should be more than two.
It's quite apparent that for any water to get stored within a area, first it should be enclosed inside the boundary of at least 2 towers. Hence there should be a minimum of 3 towers.

Clue 2: Block in ascending and descending order cannot form gap and hence cannot trap water.

Clue 3: Water the height for trapped water will depend on the minimum height between its left or right wall.

Combining all these information we can understand that trapped water for a block will be
(Min(Max left side block height, Max of right side block height) - Current Block height) * area of block.
As area of block will always be one so eventually it will be

Trapped Water On Block = Min(Max_Left_Block, Max_Right_Block)

To solve the problem we can can create a leftSideArray, which will determine the max height of block, left to the current block and max height of block, right to the current block.

Solution in Javascript

var trap = function(height) {
    if(height.length < 3) {
        return 0
    }
    let leftArray = findLeftMaxWall(height)
    let rightArray = findRightMaxWall(height)
    let trapArray = []
    let totalTrappedWater = 0
    let i  = 0
    let blockAreaWithTrappedWater = 0
    while(i < height.length){
        if(leftArray[i] == 0 || rightArray[i] == 0 || Math.min(leftArray[i], rightArray[i]) < height[i]){
            blockAreaWithTrappedWater = 0  
        } else{
            blockAreaWithTrappedWater = Math.min(leftArray[i], rightArray[i]) - height[i]
        }
        trapArray.push(blockAreaWithTrappedWater)
        totalTrappedWater += blockAreaWithTrappedWater
        i++
    }
    console.log(`trapArray, ${trapArray}`);
    return totalTrappedWater
};
// Forming Max left Array
var findLeftMaxWall = function(height) {
    let i  = 0
    let leftArray  = []
    let maxHeightLeft = 0
    while(i < height.length){
        if(i - 1 >= 0 && height[i-1] > maxHeightLeft){
            maxHeightLeft = height[i-1]
        }
        leftArray.push(maxHeightLeft)
        console.log(`leftArray:, ${leftArray}`);
        i++  
    }
    return leftArray
};
// Forming Max right Array
var findRightMaxWall = function(height) {
    let i  = height.length - 1
    let rightArray  = []
    let maxHeightRight = 0
    while(i >= 0){
        if(i+1 <= height.length - 1 && height[i+1] > maxHeightRight){
            maxHeightRight = height[i+1]
        }
        rightArray[i] = maxHeightRight
        console.log(`rightArray:, ${rightArray}`);
        i-- 
    }
    return rightArray
};
console.log(trap([0,1,0,2,1,0,1,3,2,1,2,1]))
// Answer is 6

Solution in Python

# Function to return the maximum
# water that can be stored
def maxWater(arr, n):

    # To store the maximum water
    # that can be stored
    res = 0
    # For every element of the array
    for i in range(1, n - 1):

        # Find the maximum element on its left
        left = arr[i]
        for j in range(i):
            left = max(left, arr[j])

        # Find the maximum element on its right
        right = arr[i]

        for j in range(i + 1, n):
            right = max(right, arr[j])

        # Update the maximum water
        res = res + (min(left, right) - arr[i])

    return res

#Driver code
if __name__ == "__main__":

    arr = [0, 1, 0, 2, 1, 0,
           1, 3, 2, 1, 2, 1]
    n = len(arr)

    print(maxWater(arr, n))