Quick Sort
Like Merge sort, Quick Sort uses a divide and conquer algorithm. It picks a pivot point and divides the whole array around that point. After dividing the whole array around that point we will have two parts of the array the left and the right part. Now we have to repeat the whole process for both halves i.e pick the pivot point and divide the whole array around that point. Repeating these steps will lead to a point where the array will contain only one element and that is our base case i.e when the length of the array became 1 we simply return the array.
How to find Pivot Index.
A pivot number is defined as the number whose left side is the smaller and right side is greater.
For example in arr = [2, 1, 3, 6, 4] 3 is pivot point. Because all the elements before 3 are smaller than 3 and all the numbers after 3 are greater.
To divide the array around the pivot point we need to find the pivot index i.e index of the pivot point.
For example if arr = [2, 1, 3, 6, 4]. Here pivot number = 3 and it's index = 2. After dividing the array around 3 arr_left = [2, 1, 3] and arr_right = [6, 4]
In this algorithm, we need to select a number and make it a pivot point i.e we need to put it in its right position. We can select any number we want, but for simplicity, I am going to choose the 1st element i.e element at index 0.
def pivot(arr: list) -> int:
pivot_count, length = 0, len(arr)
for i in range(1, length):
if arr[0] > arr[i]:
pivot_count += 1
arr[i], arr[pivot_count] = arr[pivot_count], arr[i]
arr[0], arr[pivot_count] = arr[pivot_count], arr[0]
return pivot_count
In above code pivot_count returns the pivot index.
Logic
How to put the selected number in the right place. Suppose we have arr = [4, 8, 2, 1, 5, 7, 6, 3]. Let's choose 4 as our number. 4 will be in its right place if all the element left to 4 is smaller and all the elements right to 4 is greater. Therefore the length of the left side of 4 = total number which is smaller than 4 and hence the index of 4 i.e pivot_index = total number which is smaller than 4 (we didn't add 1 because the index start from 0).
Therefore final array will become arr = [3, 2, 1, 4, 8, 5, 7, 6]
Dry Run
Let's dry run the above code to understand it much better.
Let arr = [4, 8, 2, 1, 5, 7, 6, 3]
Pivot_count = 0, length = 8
Beginning of Loop. Our pivot number is 4 (as I mentioned above I am going to choose the first element). We don't want to compare 4 with 4 i.e arr[0] with arr[0] that's why I am starting loop from index 1.
First iteration: 4 > 8 ---> false.
pivot_count = 0
- Second iteration: 4 > 2 ---> true. Therefore we increment the pivot_count and now we are ready to swap. Notice I am incrementing pivot_count before swapping. This is because I want to swap with the number which is the first largest number than 4. Now the
arr = [4, 2, 8, 1, 5, 7, 6, 3]
pivot_count = 1
- Third iteration: 4 > 1 ---> true. Therefore we increment the pivot_count and swap the two number.
pivot_count = 2 arr = [4, 2, 1, 8, 5, 7, 6, 3]
- Fourth iteration: 4 > 5 ---> false.
pivot_count = 2 arr = [4, 2, 1, 8, 5, 7, 6, 3]
- Fourth iteration: 4 > 7 ---> false.
pivot_count = 2 arr = [4, 2, 1, 8, 5, 7, 6, 3]
- Fourth iteration: 4 > 6 ---> false.
pivot_count = 2 arr = [4, 2, 1, 8, 5, 7, 6, 3]
- Third iteration: 4 > 3 ---> true. Therefore we increment the pivot_count and swap the two number.
pivot_count = 3 arr = [4, 2, 1, 3, 5, 7, 6, 8]
- Now the loop will break and we put the 4 at index = pivout_count
arr = [3, 2, 1, 4, 5, 7, 6, 8]
Implementing Quick sort
What we need to do
Take the first element of the array and make it pivot i.e place it in the right position. Now we have one element sorted. We divide the pivot about this point and find the pivot in the left and right half respectively. We will continue this process until the length of an array became 1.
def quick_sort(arr: list) -> list:
length = len(arr)
if length <= 1:
return arr
mid = pivot(arr)
return quick_sort(arr[:mid + 1]) + quick_sort(arr[mid + 1:])
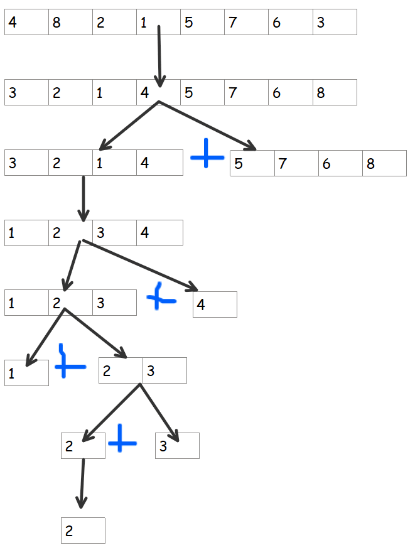
Let's dry run the program to understand it much better.
Let arr = [4, 8, 2, 1, 5, 7, 6, 3]
We will return the arr if the length of arr <= 1. This will be our base case
1 ---> arr = [4, 8, 2, 1, 5, 7, 6, 3]
mid = 3 arr = [3, 2, 1, 4, 5, 7, 6, 8]
quick_sort([3, 2, 1, 4]) + quick_sort([5, 7, 6, 8])
1->2 ---> arr = [3, 2, 1, 4]
mid = 2 arr = [1, 2, 3, 4]
quick_sort([1, 2, 3]) + quick_sort([4])
1->2->3 ---> arr = [1, 2, 3]
mid = 0 arr = [1, 2, 3]
quick_sort([1]) + quick_sort([2, 3])
1->2->3->4 ---> arr = [1]
returns [1]
1->2->3 ---> arr = [1, 2, 3]
mid = 0 arr = [1, 2, 3]
[1] + quick_sort([2, 3])
1->2->3->4 ---> arr = [2, 3]
mid = 0 arr = [2, 3]
quick_sort([2]) + quick_sort([3])
1->2->3->4->5 ---> arr = [2]
returns [2]
1->2->3->4 ---> arr = [2, 3]
mid = 0 arr = [2, 3]
[2] + quick_sort([3])
1->2->3->4->5 ---> arr = [3]
returns [3]
1->2->3->4 ---> arr = [2, 3]
mid = 0 arr = [2, 3]
[2] + [3]
1->2->3 ---> arr = [1, 2, 3]
mid = 0 arr = [1, 2, 3]
[1] + [2, 3]
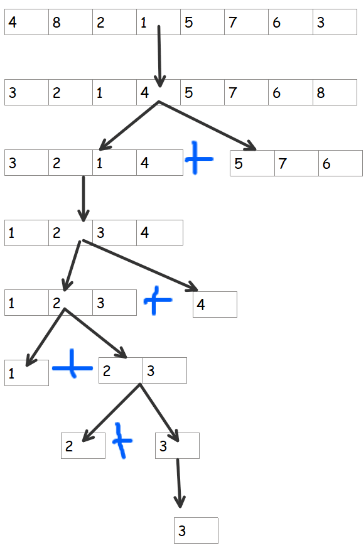
1->2 ---> arr = [3, 2, 1, 4]
mid = 2 arr = [1, 2, 3, 4]
[1, 2, 3] + quick_sort([4])
1->2->3 ---> arr = [4]
returns [4]
1->2 ---> arr = [3, 2, 1, 4]
mid = 2 arr = [1, 2, 3, 4]
[1, 2, 3] + [4]
1 ---> arr = [4, 8, 2, 1, 5, 7, 6, 3]
mid = 3 arr = [3, 2, 1, 4, 5, 7, 6, 8]
[1, 2, 3, 4] + quick_sort([5, 7, 6, 8])
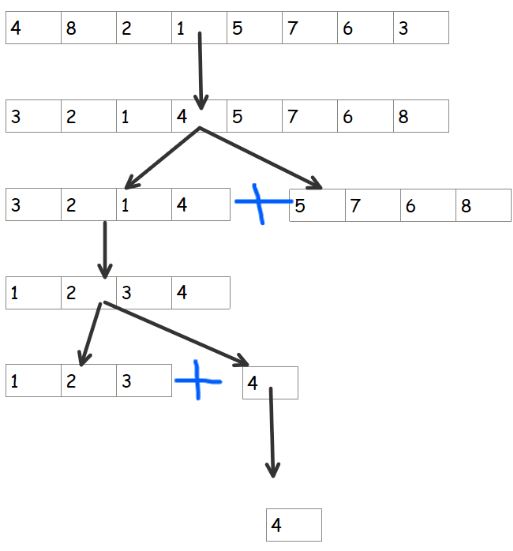
1->2---> arr = [5, 7, 6, 8]
mid = 0 arr = [5, 7, 6, 8]
quick_sort([5]) + quick_sort([7, 6, 8])
1->2->3---> arr = [5]
returs [5]
1->2---> arr = [5, 7, 6, 8]
mid = 0 arr = [5, 7, 6, 8]
[5] + quick_sort([7, 6, 8])
1->2->3---> arr = [7, 6, 8]
mid = 1 arr = [6, 7, 8]
quick_sort([6, 7]) + quick_sort([8])
1->2->3->4---> arr = [6, 7]
mid = 0 arr = [6, 7]
quick_sort([6]) + quick_sort([7])
1->2->3->4->5---> arr = [6]
returns [6]
1->2->3->4---> arr = [6, 7]
mid = 0 arr = [6, 7]
[6] + quick_sort([7])
1->2->3->4->5---> arr = [7]
returns [7]
1->2->3->4---> arr = [6, 7]
mid = 0 arr = [6, 7]
[6] + [7]
1->2->3---> arr = [7, 6, 8]
mid = 1 arr = [6, 7, 8]
[6, 7] + quick_sort([8])
1->2->3->4---> arr = [8]
returns [8]
1->2->3---> arr = [7, 6, 8]
mid = 1 arr = [6, 7, 8]
[6, 7] + [8]
1->2---> arr = [5, 7, 6, 8]
mid = 0 arr = [5, 7, 6, 8]
[5] + [6, 7, 8]
1 ---> arr = [4, 8, 2, 1, 5, 7, 6, 3]
mid = 3 arr = [3, 2, 1, 4, 5, 7, 6, 8]
[1, 2, 3, 4] + [5, 6, 7, 8]
final ans = [1, 2, 3, 4, 5, 6, 7, 8]
Final code
def pivot(arr: list) -> int:
pivot_count, length = 0, len(arr)
for i in range(1, length):
if arr[0] > arr[i]:
pivot_count += 1
arr[i], arr[pivot_count] = arr[pivot_count], arr[i]
arr[0], arr[pivot_count] = arr[pivot_count], arr[0]
return pivot_count
def quick_sort(arr: list) -> list:
length = len(arr)
if length <= 1:
return arr
mid = pivot(arr)
return quick_sort(arr[:mid + 1]) + quick_sort(arr[mid + 1:])
print(quick_sort([4, 8, 2, 1, 5, 7, 6, 3]))




















Top comments (0)