Introduction
The sliding window technique is used for reducing some redundant calculations that slow down the program. like it can reduce time complexity from O(n^2) to O(n) with O(1) space complexity.
Why use it?
First of all it reduce time coplexity and also with O(1) space complexity. so let's understand with Example..
So we want to find maximum sum of k consecutive integer from array, so brute force would look like this for k=5,
#include<iostream>
#include<vector>
using namespace std;
int main(){
vector<int> arr = {5,2,6,7,7,3,2,1,3,9};
int final_max = 0;
for(int i=0;i<arr.size()-5;i++){
int temp_max = 0;
for(int j=i;j<i+5;j++){
temp_max += arr[j];
}
if(temp_max>final_max){
final_max = temp_max;
}
}
cout << final_max << endl;
return 0;
}
But time complexity of the above program is O(nk)
Brute Force Approach

As per we can see in the above image brute approach checks every pattern of k length(here k=5). if you compare the above code with this image you will understand it.
here k=5 so it won't make too much difference in O(n) and O(nk) but what if k is too big. then it will impact the running time of the program, so what to do now? can we implement the above code to O(n)?
The answer is YES!! , with the use of the sliding window, we can reduce the time complexity of the above code O(n).
How does Sliding Window Works?
So let's see how sliding window works.
let me give you simple visual with small array,
{5,2,6,7,7,3,2,1,3,9}
for k=3 (because k=5 is too much to write)
{5,2,6} --> first 3 elements
{2,6,7} --> remove 5 and add 7
{6,7,7} --> remove 2 and add 7
{7,7,3} --> remove 6 and add 3
{7,3,2} --> remove 7 and add 2
{3,2,1} --> remove 7 and add 1
{2,1,3} --> remove 3 and add 3
{1,3,9} --> remove 2 and add 9
let's understand with second example,
{5, 7, 1, 4, 3, 6, 2, 9, 2}
k=5
{5,7,1,4,3} --> first 5
{7,1,4,3,6} --> remove 5 and add 6
and so on.
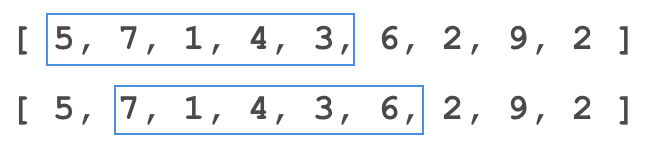
As we can see in the above image it moves one step at one time. so this is how actually it works.
Let's Code
Code for a maximum sum of k consecutive integer from the array, using the sliding window technique.
#include<iostream>
#include<vector>
using namespace std;
int sum_of_k_ele(vector<int> arr,int k){
int sum = 0;
for(int i=0;i<k;i++){
sum += arr[i];
}
return sum;
}
int main(){
vector<int> arr = {5,2,6,7,7,3,2,1,3,9};
int k=3;
// below function will be used only once
// for finding sum of first k digits
int final_sum = sum_of_k_ele(arr,k);
int temp_sum = final_sum;
for (int i=k;i<arr.size();i++){
temp_sum = temp_sum - arr[i-k];
temp_sum = temp_sum + arr[i];
if(temp_sum>final_sum){
final_sum = temp_sum;
}
}
cout << final_sum << endl;
return 0;
}
When to use?
When you are looking for a subrange in a given string or array-like highest or smallest value or targeted value.
it involves data structure which is iterable like string or array.
when there can be brute force solution with O(n^2) or (2^n)
More Examples...
Note : Solutions in above questions are just plain code.
## References
Thank You 😊😊


Top comments (0)