Welcome to the SQL showdown series!
What is this and how does it work?
I'm committing to publishing a SQL challenge every day for 30 days. In each post I'll describe my solution to the last day's challenge. I'll follow that up with a full description of the challenge for the next day.
Write your own solution in the comments! Let's see who can come up with the most creative solutions.
Challenge #14: UFO Sightings
For a bit of fun I decided to load an open data-set of UFO sightings into PostgreSQL. Each row represents a reported sighting, including the date, shape of the object, and the duration of the sighting.
Let's see if we can deduce some kind of seasonal pattern to UFO sightings. Here's the challenge itself:
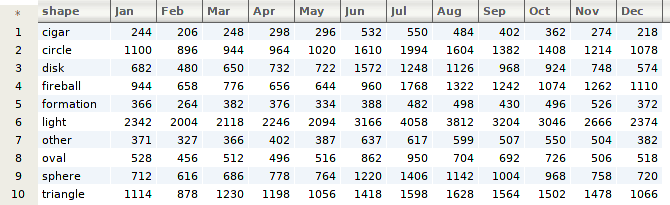
Given UFO sightings from 1906 to present day, can you produce a monthly count of sightings by shape?
Here's an example of the output we should get:
Sandbox Connection Details
I have a PostgreSQL database ready for you to play with.
The password is the same as the username! To query the ufo table:
SELECT * FROM day14.ufo;
Solution to Challenge #13: Permutations
This was the challenge from yesterday:
Can you generate all of the permutations of a given set in SQL?
Specifically, we wanted all of the permutations from the set {1, 2, 3}. My first thought here was to use a CROSS JOIN, as that kind of join will produce every possible pairing between two tables.
That's not quite what we want, however, because we'd like each item in the permutation to be distinct. In other words, {1, 1, 1} is not a valid permutation. Luckily, that's not too hard to enforce by means of a WHERE clause.
Let's take a look.
WITH v AS (
SELECT generate_series(1, 3) AS n
)
SELECT * FROM v AS v1
CROSS JOIN v AS v2
CROSS JOIN v AS v3
WHERE
v1 NOT IN (v2, v3) AND
v2 NOT IN (v1, v3) AND
v3 NOT IN (v1, v2);
The WHERE clause checks that each element of the permutation does not equal any other element, thus ensuring that there's no repetition.
You would need to add more joins to account for a larger set. Can anyone think of an approach that works no matter the size of the input set?
Good luck!
Have fun, and I can't wait to see what you come up with! I'll be back tomorrow with a solution to this problem and a new challenge.



Top comments (0)