Internally, each neuron inside a neural network detect patterns or characteristics inside your data for feeding back to other neurons. I pretend to show you how neural networks can learn to solve a problem, and what is our tasks as developers in this learning process. First, we review typical mathematical concepts used for training neural networks and next, I will explain the algorithms that permit the learning task.
For understanding the content of this post, you should read my last article, where I explain in detail the machine learning and deep learning problem of how the base neural network's architecture is.
At this point, we know that a learning process consists in finding the weights of the net that better estimate the values of a function, but what is the real problem that we are solving? For answer this questions, we need to define some mathematical concepts of mathematical functions analysis.
Derivate of a function
At this point you could be thinking “WTF is this? I arrive to this post for learning deep learning and this guy start with a math class” and my answer is “Yes, but relax because you only need to understand the concepts because in a real world problem probably you will use neural networks and no research about these”.
Returning to the problem, the derivative of a function represent the tangent line that pass for this point, and it can be interpreted as slope. If you drop a ball at this point, the ball will go to the direction of the derivate, and this concept is the gradient.
Gradient
The gradient is a derivative of a function, but with direction and step magnitude. It is like the velocity of the ball, it always goes to the bottom of the line but with the velocity that you can set up. Mathematically this is more complicated, but the concept is sufficient.
And now we know how to calculate the derivate of function and the direction of the derivative, but if you look at each derivate of function, you will notice that each gradient point to a minimal point of a function. A minimal point is a point where the function return a low value. If this value is the lower, it will be the minimal value and if not, it will be a partial minimal value. And you think this more, you can implement an algorithm that can find any minimal point of a function from any point in a function moving in the direction of the gradient and this algorithm is the gradient descent.
Gradient Descent
Gradient descent is a mathematical algorithm that permit to find the minimal of a function moving in the direction of the gradient. The steps of this algorithm are:
- Calculate the gradient at the actual point.
- Look at the direction of the gradient.
- Move actual point following this direction with a step size.
- Execute step 1, 2 and 3 until a number of iterations.
The process is illustrated in this image:
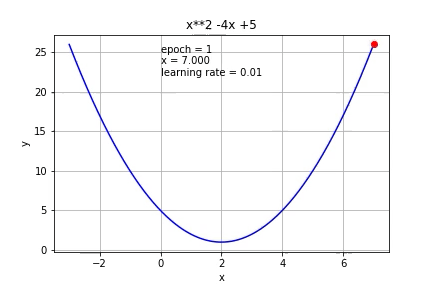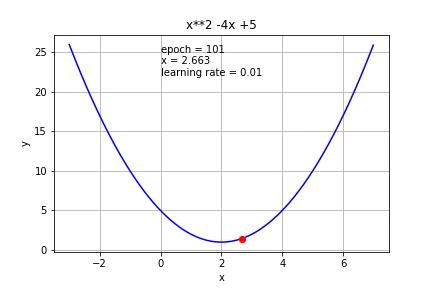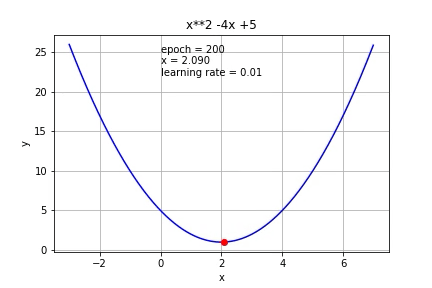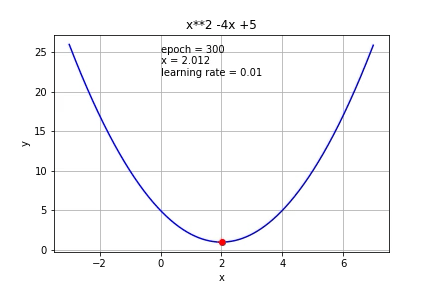This algorithm resolve an optimization problem in which you want to find a minimal value inside a function, but how can apply this method to network's learning process. So first, we need to define a function to minimize (cost function) and the network will learn the weights that minimize this function. This function link the outputs of the network with the value that we expect. Next, we calculate the gradient but for each weight of the network (this is back propagation because you need the next neurons gradients for calculating it) and finally, we advance on the direction of the gradient with a step size.
This process is repeated over a number of epochs, and it's the process of training.
Top comments (0)