I guess the most popular programming paradigm is the imperative programming, but it is not the only kind of programming, e.g. functional programming is famous too. Constraint programming is not so popular. But it is very powerful tool to solve combinatorial problems. Instead of implementing the algorithm which solves the problem and then spend a lot of time on debugging, refactoring and optimizing it, constraint programming allows you just describe the model in its own syntax and special program (solver) will find the solution for you (or says if there isn't any). Isn't it cool? When I first met it I was fascinated with such possibility.
Minizinc
Probably the most used constraint programming tool (at least for educational propose) is Minizinc. It provides IDE for model declaration and several built-in solver to look for solution of them. You can download it from the official site.
Simple Model in Minizinc
Let's see an example of model solving, we will start with cryptarithmetic problem. In such kind of problem all letters should be replaced with digits with two main restriction:
- equation should be hold
- the same digit can’t be assign to different letters and vise versa.
For example let's solve the following equation:
S E N D
+ M O R E
= M O N E Y
Model structure
In minizinc every model is a collection of variables, parameters and constraints.
Variables are unknown values which should be found by solver, parameters are some constants which are known during model evaluation, you can change parameters from run to run, and this will, obviously, affect result. E.g. number of cities and distances between them are parameters for traveling salesman problem, the path will depends on them, but the programmer can create one model for the problem and then just execute it for different parameters without model source code changes.
Constraints are constraints :) which should be satisfied by variables values.
Model declaration
Lets start actual programming. Here we have 8 variables (S, E, N, D, M, O, R, Y), they are digits, so they can take values from 0 to 9 (S and M from 1 to 9, because the number can't start with 0).
In minizinc syntax this is declared by the following way:
var 1..9: S;
var 0..9: E;
var 0..9: N;
var 0..9: D;
var 1..9: M;
var 0..9: O;
var 0..9: R;
var 0..9: Y;
Next we should specify equation, in minizinc it is specified in the very common way:
constraint 1000*S + 100*E + 10*N + D
+ 1000*M + 100*O + 10*R + E
== 10000*M + 1000*O + 100*N + 10*E + Y;
We also should specify that every variable has its own values, and there shouldn't be any variables with the same value. Minizinc has specific constraint for it alldifferent, but it isn't specified in built-in functions, we should include it be special directive include "alldifferent.mzn";.
And the last thing we should do it to declare how to solve the model, there are 3 variant: satisfy, minimize and maximize, I guess their names are self-explaining :).
Resulting source code
include "alldifferent.mzn";
var 1..9: S;
var 0..9: E;
var 0..9: N;
var 0..9: D;
var 1..9: M;
var 0..9: O;
var 0..9: R;
var 0..9: Y;
constraint 1000 * S + 100 * E + 10 * N + D
+ 1000 * M + 100 * O + 10 * R + E
= 10000 * M + 1000 * O + 100 * N + 10 * E + Y;
constraint alldifferent([S,E,N,D,M,O,R,Y]);
solve satisfy;
output [" ",show(S),show(E),show(N),show(D),"\n",
"+ ",show(M),show(O),show(R),show(E),"\n",
"= ",show(M),show(O),show(N),show(E),show(Y),"\n"];
Minizinc can execute the model and find the solution:
9567
+ 1085
= 10652
By default, minizinc stops execution of satisfy problem after the first solution, this behavior can be changed in the settings, you can reexecute this model and ask minizinc to find all solution, but it will say there is only one :).
First Part Conclusion
Minizinc provides powerful, general and easy to use way to deep into constraint programming. But it uses its own syntax, which slow down the learning and make integration with other programming languages harder.
Integration with Python
minizinc-python solves the second issue, by providing the way to call minizinc models from python, the library will run minizinc, serialize your input and parse output, but the programmer still should write quite a lot lines of code. We can look at the example of solving square equation solving:
import minizinc
# Create a MiniZinc model
model = minizinc.Model()
model.add_string("""
var -100..100: x;
int: a; int: b; int: c;
constraint a*(x*x) + b*x = c;
solve satisfy;
""")
# Transform Model into a instance
gecode = minizinc.Solver.lookup("gecode")
inst = minizinc.Instance(gecode, model)
inst["a"] = 1
inst["b"] = 4
inst["c"] = 0
# Solve the instance
result = inst.solve(all_solutions=True)
for i in range(len(result)):
print("x = {}".format(result[i, "x"]))
Personally for me it is a problem to remember and recreate such example, and minizinc model (which is just 4 lines of code) is represented as a string, so IDE and python can't highlight the syntax and provide any help and checks for you.
There Must be a Better Way
Why don't we hide all solver lookup and parameter instantiation as well as provide the way to implement models on pure python?
This is what zython (miniZinc pYTHON) does. It is the most simply way to drive into constraint programming.
**from the ways I know
**at least if you are a python developer. :)
Getting Started
To start with zython you should have python 3.6+ and minizinc installed into the default location or available in $PATH.
pip install zython
python
>>> import zython as zn
If everything was installed correctly, there shouldn't be any errors and you can start to play with zython.
Send More Money
At first lets look at the model, we already know - Send More Money problem.
import zython as zn
class MoneyModel(zn.Model):
def __init__(self):
self.S = zn.var(range(1, 10))
self.E = zn.var(range(0, 10))
self.N = zn.var(range(0, 10))
self.D = zn.var(range(0, 10))
self.M = zn.var(range(1, 10))
self.O = zn.var(range(0, 10))
self.R = zn.var(range(0, 10))
self.Y = zn.var(range(0, 10))
self.constraints = [(self.S * 1000 + self.E * 100 + self.N * 10 + self.D +
self.M * 1000 + self.O * 100 + self.R * 10 + self.E ==
self.M * 10000 + self.O * 1000 + self.N * 100 + self.E * 10 + self.Y),
zn.alldifferent((self.S, self.E, self.N, self.D, self.M, self.O, self.R, self.Y))]
model = MoneyModel()
result = model.solve_satisfy()
print(" ", result["S"], result["E"], result["N"], result["D"])
print(" ", result["M"], result["O"], result["R"], result["E"])
print(result["M"], result["O"], result["N"], result["E"], result["Y"])
It should return the same result as before. It has still pretty a lot of code, isn't it? But if we look more precise we will see, it is mostly variable declaration and arithmetic equation, zython makes all dirty work as finding solver, instantiation parameters, parsing result and running model. All you do is the programming itself. As well zython provides python syntax for model definition, which makes it possible for IDE to highlight your code and check it for errors before running. Zython provides additional checks and error messages during execution.
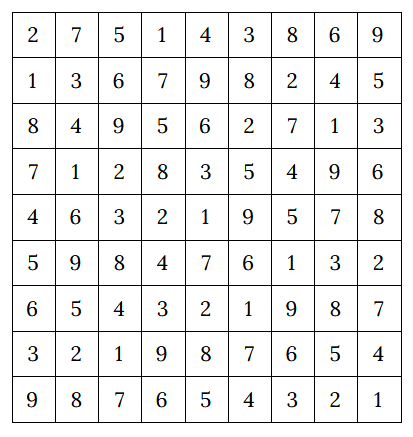
Sudoku generation
Lets generate sudoku field. We should use zn.Array for it. Array can be both variable and parameter, in this model it is variable, as we don't now the values and want to find them.
import zython as zn
class MyModel(zn.Model):
def __init__(self):
self.a = zn.Array(zn.var(range(1, 10)), shape=(9, 9))
self.constraints = \
[zn.forall(range(9),
lambda i: zn.alldifferent(self.a[i])),
zn.forall(range(9),
lambda i: zn.alldifferent(self.a[:, i])),
zn.forall(range(3),
lambda i: zn.forall(range(3),
lambda j: zn.alldifferent(self.a[i * 3: i * 3 + 3, j * 3: j * 3 + 3]))),
]
model = MyModel()
result = model.solve_satisfy()
print(result["a"])
The model should produce something like it:
Traveling Salesman (or Salesperson?) Problem
As I promise we will look at TSP model, it can be declared with the following way:
import zython as zn
class TSP(zn.Model):
def __init__(self, distances):
self.distances = zn.Array(distances)
self.path = zn.Array(zn.var(range(len(distances))),
shape=len(distances))
self.cost = (self._cost(distances))
self.constraints = [zn.circuit(self.path)]
def _cost(self, distances):
return (zn.sum(range(1, len(distances)),
lambda i: self.distances[self.path[i - 1],
self.path[i]]) +
self.distances[self.path[len(distances) - 1],
self.path[0]])
distances = [[0, 6, 4, 5, 8],
[6, 0, 4, 7, 6],
[4, 4, 0, 3, 4],
[5, 7, 3, 0, 5],
[8, 6, 4, 5, 0]]
model = TSP(distances)
result = model.solve_minimize(model.cost)
print(result)
We again used array in the model, but now it is a parameter, which means its values defined before model execution.
Second Part Conclusion
Constraint programming is worth to know paradigm of programming, which can save a lot of time on solving a lot of problem: create schedule, determine which units should be hire to own the strongest army for such amount of resources in your favorite strategy, or what is the strongest build in your favorite RPG, what colors you should use to brush the geographical regions on the map in a way, that all adjacent regions will have different color, and even what is the base timeslot for public transport and which cakes you should bake to maximize your bakery profit.
Zython provide the way to express constraint programming model in pure python and easily solve it. You can see more examples in documentation.
I would like to hear your opinion about this library, don't hesitate to report bug and feature request as will as collaborate and create PR.
Good luck in constraint programming learning.




Top comments (0)