Tron game 🏍️ - A Combinatorial search in python

About Tron game:

Tron is a two player game based on the popular movie Tron. The objective of the game is to cut off players movement through each others motorbikes that leave a wall behind them as they move.

Like this:

I came across this question in Hackerrank, where our programs will read the players position at each turn and will decide the movement, by printing one of (LEFT, RIGHT, UP, DOWN) to the console, and we can see the result visually.

Before we go further, I should tell you that the solution below is a naive and basic approach (scored 36/50) and there are a lot of algorithms available that provide better results.

Now the input we get are:

• player's turn
• bot player's current positions
• the whole grid (15x15) values

Input is:

r
4 3 5 13
###############
#-rr--------gg#
#-rr--------gg#
#-rr--------gg#
#-rr--------gg#
#-r---------g-#
#-r---------gg#
#rr----------g#
#-------------#
#-------------#
#-------------#
#-------------#
#-------------#
#-------------#
###############

We will read the grid into a matrix like representation, where grid[0][1] means 1st row's second column.

Now the actual code ...
First reading the input part:

current_player =  input() # player_id (whose turn is it)

# here we are reading both players' positions
player_pos = input().split(" ")
player_pos = list(map(int, player_pos))
rpos = [player_pos[0], player_pos[1]]
gpos = [player_pos[2], player_pos[3]]
grid_size = 15

grid = [] # reading grid into an array
for gr in range(grid_size):
    grid.append(input())

Now to the important part, we have the player's current positions and where they went earlier from the grid, using this information we have to decide what direction we choose to move ahead by one step, so that we can avoid getting trapped and trap other opponents.

The following code, calculates how much free (movable) space available at each direction and chooses the direction which has the most free space. (Hoping it can help avoid traps), this is done at each iteration.

lets write code to calculate the free space...

# Here were writing code, that actually makes the decision
def calculate_free_steps(grid, pos):
    """
    Reads the current grid state, and current player's position
    and returns a dictionary with free spaces in each direction.
    returns: {"LEFT":4, "RIGHT":5, "UP":9, "DOWN":0}
    """
    # we are initializing the free steps
    # l = free steps available in left direction
    l = r = u = d = 0

    # We're calculating free steps in each direction
    # i.e., places in grid having '-' as value

    # reading player's current row & current column values
    row, col = pos[0]-1, pos[1]

    # calculating free steps in upward direction
    # if row is > 0, we can try to go 'UP'
    while row > 0:
        # if cell is '-', increment up_free_steps
        if grid[row][col] == "-":
            u += 1
            row -= 1 # go to top row
        else: # if cell is not '-' means it's not free
            break # so break the loop

    # do the same for 'DOWN'
    row, col = pos[0]+1, pos[1]
    # calculating free steps available in 'DOWN' direction       
    while row < len(grid):
        if grid[row][col] == "-":
            d += 1
            row += 1
        else:
            break

    # now for 'RIGHT'
    row, col = pos[0], pos[1]+1
    while col < len(grid[0]): #right
        if grid[row][col] == "-":
            r += 1
            col += 1
        else:
            break

    # and finally for 'LEFT'
    row, col = pos[0], pos[1]-1
    while col > 0: # left
        if grid[row][col] == "-":
            l += 1
            col -= 1
        else:
            break

    # returning the free steps for each direction
    return {"LEFT":l, "RIGHT":r, "UP":u, "DOWN":d}

Now to the final and main part of the code..

We have the free steps available in each direction, how do we choose which direction to go...🤔🤔🤔?

For simplicity we will just pick the direction which has most free steps.

🙏 Do note this is not an ideal solution, comments are welcome. 🙏

direction_to_go = None # initially unknown
free_steps_available = 0

# read the current player's position
ppos = rpos if current_player == "r" else gpos

# calling the method we created above
free_steps_data = calculate_free_steps(grid, ppos)

# looping each direction
# and choosing the one with max free steps
for direction in free_steps_data:
    if free_steps_data[direction] > free_steps_available:
        direction_to_go = direction
        free_steps_available = free_steps_data[direction]

# finally printing to the console
print(direction_to_go)

output will be like:

DOWN

Following are the couple of visualization of the game (We are blue)

Won:

Lost:

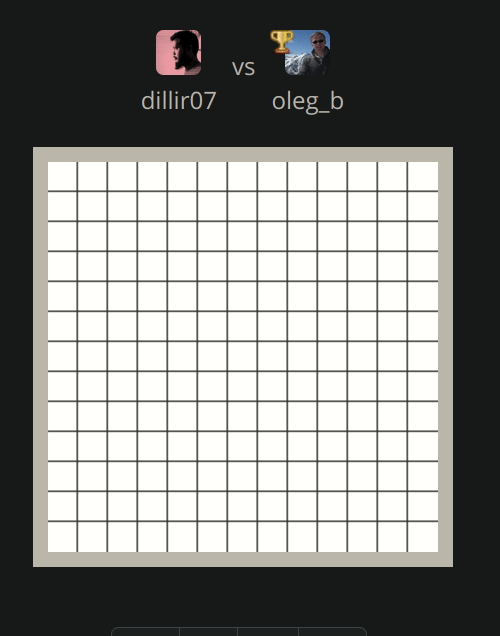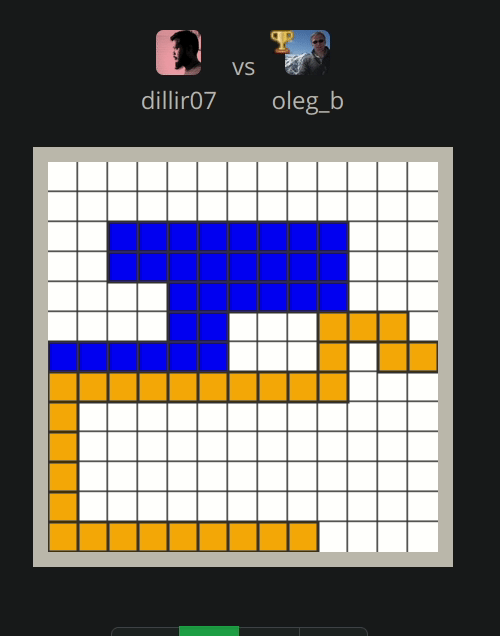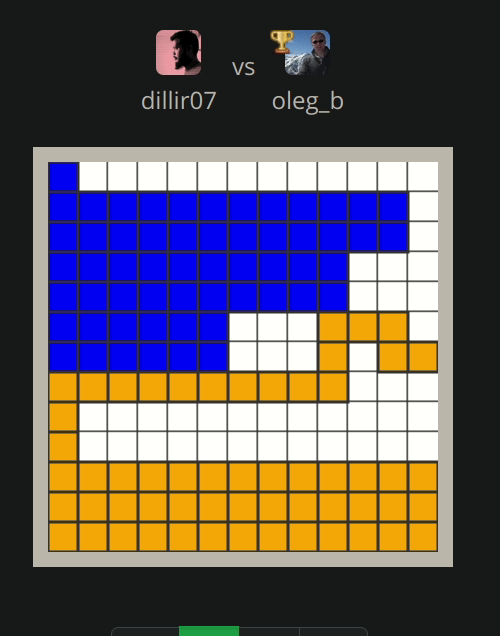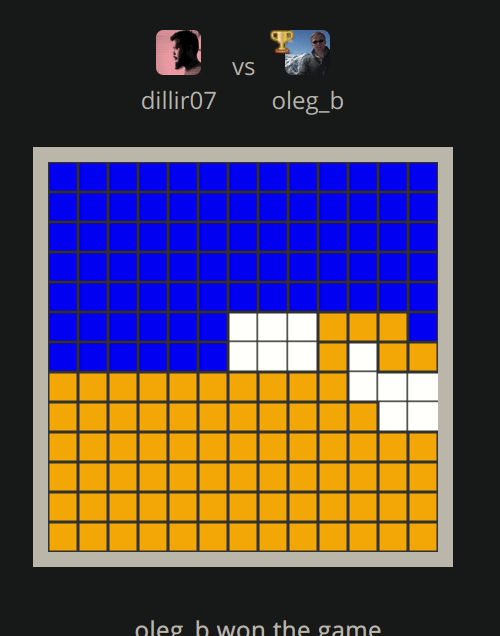
Author (orange) written a nice algorithm to fill as much space as possible by avoiding opponent, so opponents can run out of space and trap themselves.

Thank you for reading.. comments & suggestions are welcome.