Depth First Traversal in Binary Trees
Hello!
In an effort to teach myself fundamentals that I might have missed in my rudimentary yet effective bootcamp experience, I'm going to cover some basics in a series about data structures and algorithms. As you might have surmised, in this post we're going to be discussing depth first traversal
A depth first traversal is a way of accessing every node in graph or binary tree.
A depth first traversal is characterized by the direction of the traversal.
In other words, we traverse through one branch of a tree until we get to a leaf, and then we work our way back to the trunk of the tree.
In this post, I'll show and implement three types of depth first traversal.
Inorder traversal
As 'depth first' implies, we will reach the 'leaf' (a node with no children) by traveling downward in a recursive manner.
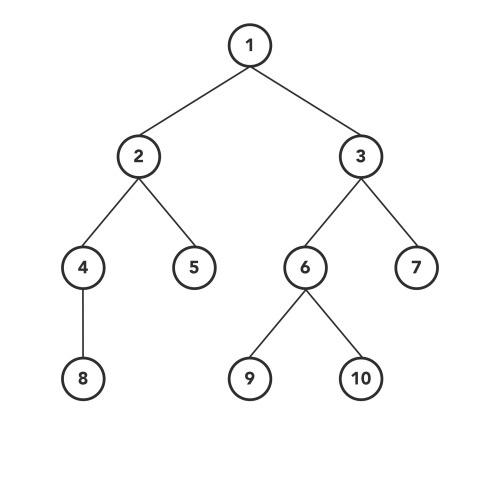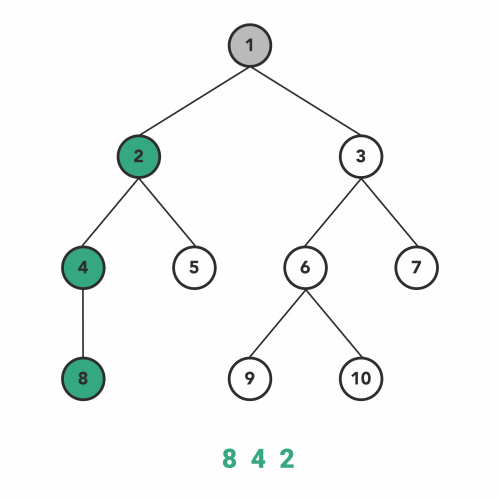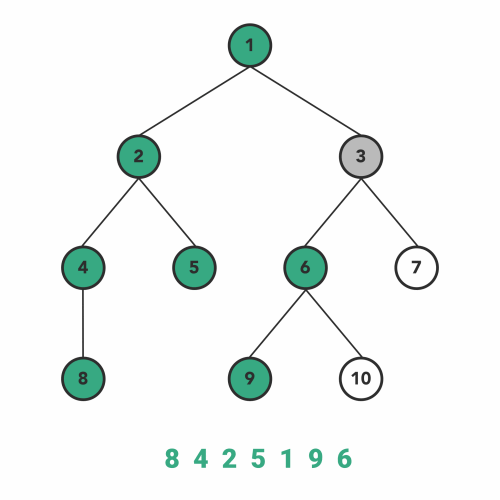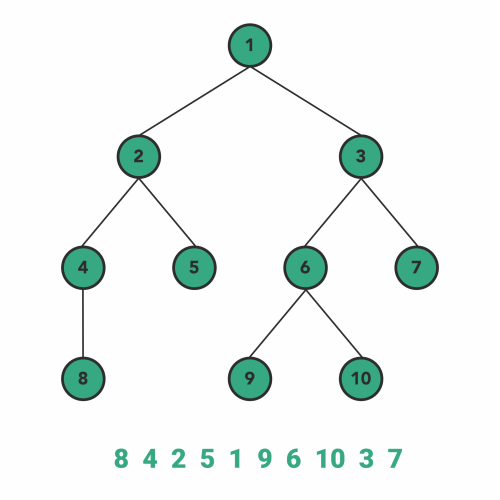
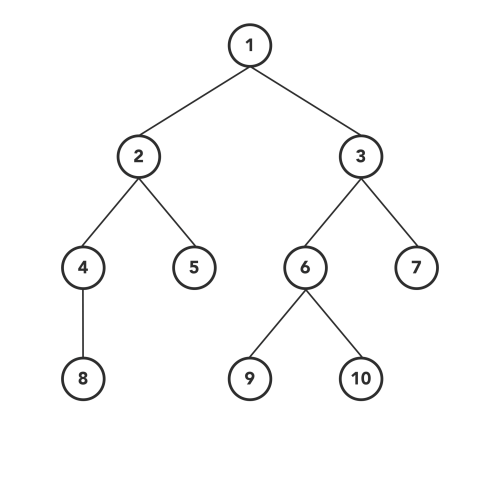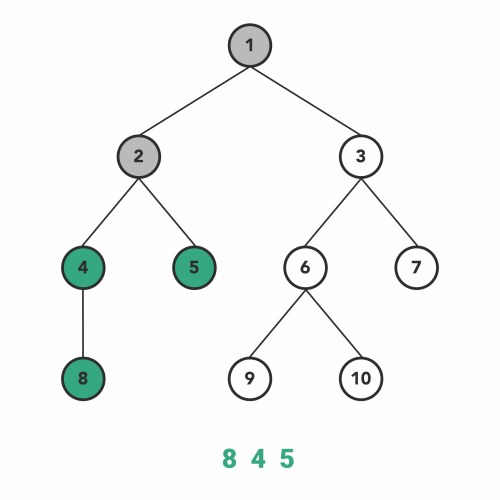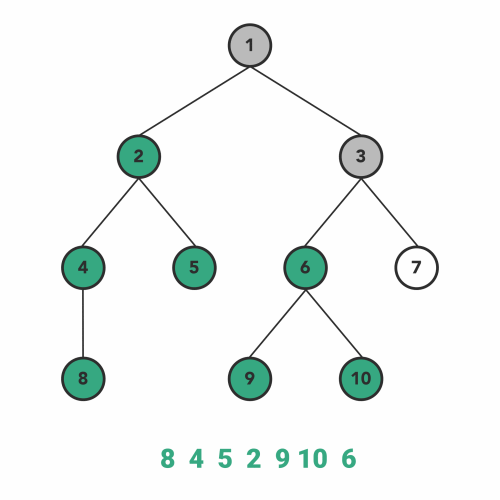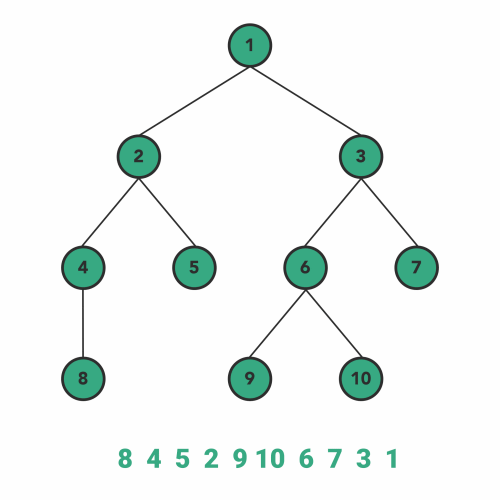
Inorder traversal adheres to the following patterns when traveling recursively:
- Go to left-subtree
- Visit Node
- Go to right-subtree
We can illustrate this concept with the follow gif
Let's code!
For the following examples we'll be using the Tree class I've defined below.
class Tree {
constructor(value, left, right) {
this.value = value;
this.left = left;
this.right = right;
}
}
Let's go ahead and create the tree we see in the example gif
tree = new Tree(
1,
new Tree(2, new Tree(4, new Tree(8)), new Tree(5)),
new Tree(3, new Tree(6, new Tree(9), new Tree(10)), new Tree(7))
);
Finally, let's implement inorder traversal:
const inOrderTraversal = (node, cb) => {
if (node !== undefined) {
inOrderTraversal(node.left, cb);
cb(node.value);
inOrderTraversal(node.right, cb);
}
};
inOrderTraversal(tree, console.log);
// 8, 4, 2, 5, 1, 9, 6, 10, 3, 7
As you can see, the code mimics the steps outlined above.
The trickiest bit of this visualization is imagining the recursion until you hit the left-most leaf. I personally groan at the sight of recursion, but it's just something that has to be confronted with depth first traversal.
Fun fact:
Inorder Traversal of Binary Search Tree will always give you Nodes in sorted manner
Preorder traversal
Preorder traversal adheres to the following patterns when traveling recursively:
- Visit Node
- Go to left-subtree
- Go to right-subtree
In other words, preorder is extremely similar to inorder except for the fact it will visit the root of the node first.
Let's implement preorder traversal:
const preOrderTraversal = (node, cb) => {
if (node !== undefined) {
cb(node.value);
preOrderTraversal(node.left, cb);
preOrderTraversal(node.right, cb);
}
};
preOrderTraversal(tree, console.log);
// 1, 2, 4, 8, 5, 3, 6, 9, 10, 7
Postorder traversal
Post traversal adheres to the following patterns when traveling recursively:
- Go to left-subtree
- Go to right-subtree
- Visit Node
Once again, postorder is extremely similar to the others except for the fact it will visit the left subtree, then the right subtree and finally the node itself.
Let's implement postorder traversal:
const postOrderTraversal = (node, cb) => {
if (node !== undefined) {
postOrderTraversal(node.left, cb);
postOrderTraversal(node.right, cb);
cb(node.value);
}
};
postOrderTraversal(tree, console.log);
// 8, 4, 5, 2, 9, 10, 6, 7, 3, 1
That wraps it up for depth first traversal...as far as I know. Please let me know if you've learned anything or I've made any egregious mistakes!
Till next time, cheers!




Top comments (0)