My PocketMoney Algorithm

When I made my first fully functioning Ruby on Rails app (on GitHub here), I wanted to create a powerful app that could answer real world questions. The question I wanted it to answer was: “How much can I spend right now? or in other words “How much money is in my pocket? (see what I did there?)
To get that answer proved a little more tricky than I at first anticipated. I have the recurring expenses from the user; I know what bills are coming up as well as how much money is coming in, and I can figure out how much spending money they would have for non fixed expenses. I can also calculate how much they have in the bank now because I have all of their non fixed expenses since the last time they gave me their bank balance. At first I thought calculating how much they could spend right now would be as easy as:

1. Calculating how much money they have in the bank right now
2. Calculating how much spending money they have that month that they haven’t already spent

Then I stopped to think about it and I realized there was another issue. What if you get paid $3,000 a month. $1,500 at the beginning and $1,500 in the middle, and your total expenses for the month are only $2,500, but your rent and car payments are all due the first week of the month totaling $1,800. You would run out of money after the first week of the month. The challenge is to find the lowest amount you would have to hold at the end of the previous month in order to meet your bills for the current month.

Buckets and Pits

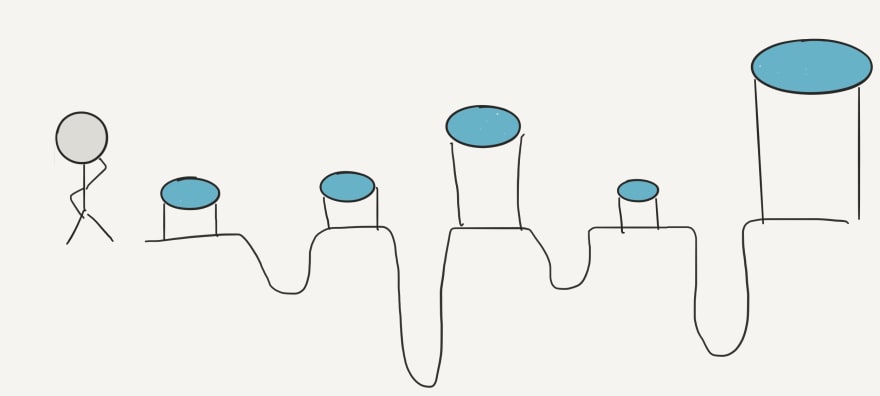
To get this number I came up with an allegory called Buckets and Pits. Imagine there is a farmer, named Farmer, and like many farmers he is very conscious of conserving water. He has a reservoir full of water and several holes in the ground along his farm that for some specific and really important reason need to be filled with water. In addition to his reservoir he also has rain barrels next to each hole that may or may not contain some water. Of course, due to the complicated nature of his method of farming, the pits and buckets are of varying sizes and rarely match each other.

So if you are with me so far, hopefully you are picturing a man standing in front of a series of buckets filled with water and empty pits of varying sizes.
Farmer, being a somewhat quirky methodical man, refuses to make multiple trips back and forth to the reservoir so he goes to each pit one at a time to see how much water he will need to take with him.

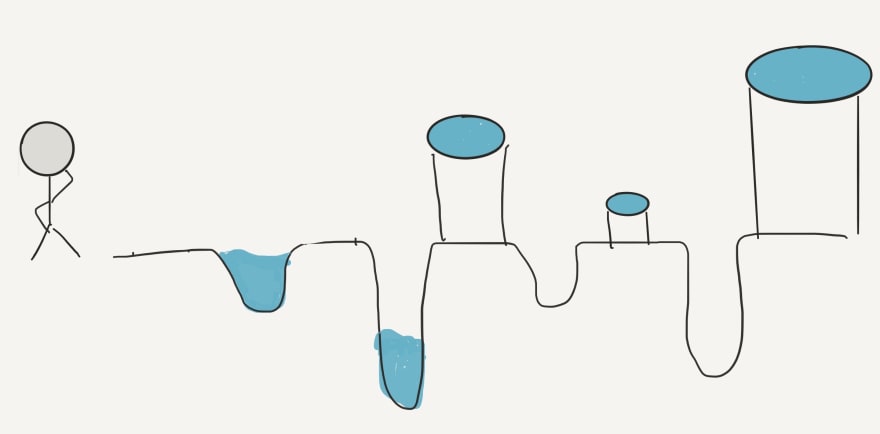
He pours the first bucket in the first pit and sees that it matches up quite nicely, with neither extra water, nor water missing. He moves on to the second pit and realizes that he is missing quite a bit of water.
You may or may not have guessed that each pair of one bucket and one pit in this allegory represent one day in my code. The water is income and the pits are expenses. You will see these netted together to represent the variable Bucket later on.
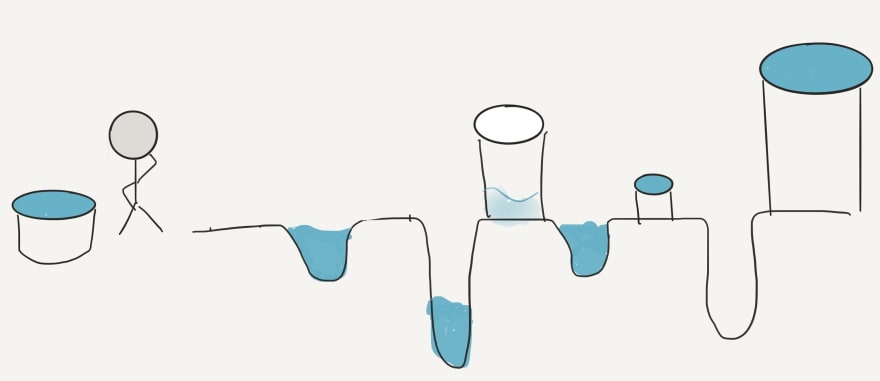
Because he is quirky, Farmer refuses to take the bucket on the third pit to use on the second pit so he goes back and fills up a larger bucket, his Reserve, with just the amount of water he will need to top off pit number 2. He then moves on and realizes that pit 3 has way more water than he needs for pit three so he keeps the extra amount to be used in pit four.

Are you with me so far? Farmer refuses to run out of water at any one pit (much as your bank account refuses to run out of money without triggering an overdraft) so he goes through and calculates exactly how much water he will need to bring in as Reserve so that that doesn’t happen. he doesn’t care about having water leftover at the end, but he does want as little water in his reserve starting out as possible.

From Allegory to Real Life

Now lets look at the code. I’ll skip the methods where I pull in the transactions and such (if you would like to see the full model click here). Let’s go through this step by step.

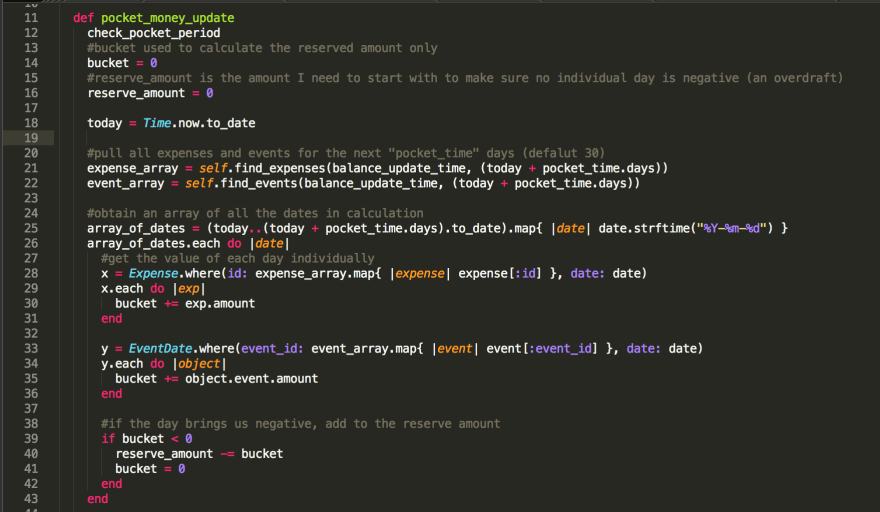
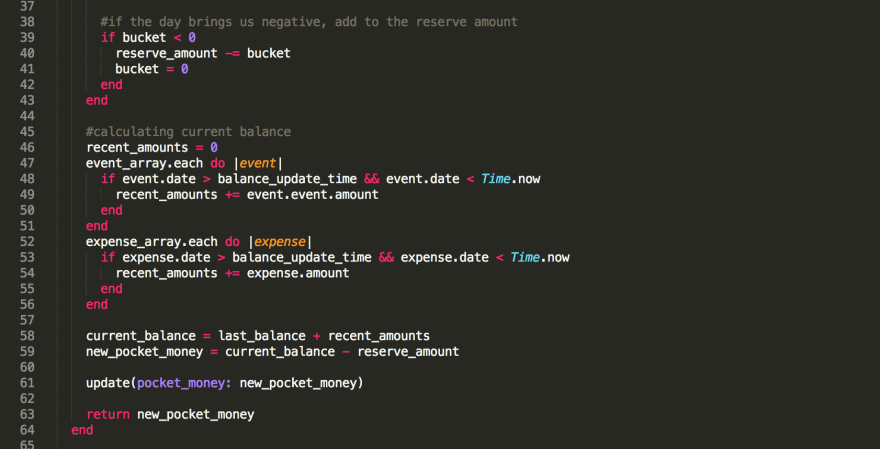
1. Lets take all of the positive and negative transactions and add them together for one day. We’ll call that a Bucket. We loop through each day of the calculation on line 26 and then loop through each related expense (x) and fixed expense/income (y) on lines 29 and 34, respectively for that day.
2. Lets see if our bucket for the day is positive or negative (line 39). If it’s positive (or zero) we can move the amount in the Bucket on to the next day. If it’s negative we need to add that amount in positive to our Reserve (reserve_amount) and set the Bucket balance to zero because we have already accounted for that deficiency in the reserve.
3. Once we have gone through all of the days, we calculate exactly how much money we have in the bank right now (i.e. the reservoir, calculated in lines 45–58) and subtract the Reserve amount from our current balance. That then becomes our PocketMoney, the amount we can spend today without defaulting on our bills in the future.

Remember, just as the Farmer doesn’t care if he has too much water at the end, we don’t care if we have extra money in our last bucket, as long as we haven’t run out along the way. Whatever is left in the bucket variable (which can only be positive) does not factor into our PocketMoney balance.
I hope you have enjoyed my little algorithm. It was a stressful joy to come up with and I am a little proud of it. However, because GitHub keeps the history and the work is never really lost, I am happy to replace it with a better one. Let me know your ideas!
As always, also let me know if you catch any bugs in the code or see something fishy. Always looking to improve and, unfortunately, my experiment in TDD did not extend into this part of the app (see my article). Maybe some day!