Walking a tree (breadth first search)

Intro

A short blog on how you can traverse a tree layer by layer. Breadth first search is an algorithm that does exactly this (also works for graphs, graph is a generalization of a tree)

breadth first search

First, imagine a tree not as a regular tree, but as an a upside down tree (I was really confused about it, because the root is on the top and not at the bottom).

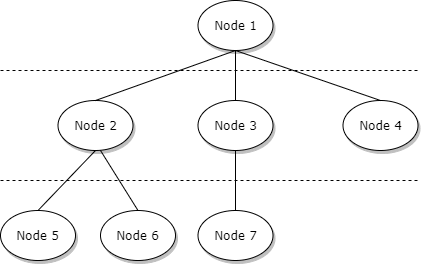
Let's take for example the following tree:

The idea is to traverse the tree layer by layer, in this case:

• first we visit the first layer, only one node here ''node 1''
• then the nodes at the second layer, ''node 2'', ''node 3'' and ''node 4''
• finally, the third layer ''node 5'', ''node 6'' and ''node 7''

js implementation

What is needed for a breadth first implementation in a tree:

1. a queue
2. a tree

the algorithm in plain english:

1. initialize an empty queue
2. take the root from the tree
3. add to queue the root node
4. while there are nodes in the queue do:
5.      take/remove the first element of the queue
6.      process the data of the current node
7.      if current node has any children add them to queue

the algorithm in js:

// a node looks like this
rootNode = {
    id: 1,
    data: 1,
    children: [secondNode, thirdNode, forthNode]
};

function breadthFirstSearch(rootNode) {
    let queue = [];
    queue.push(rootNode);

    while (queue.length !== 0) {
        // remove the first child in the queue
        currentNode = queue.shift();
        // do something cool with the data
        // printing them is also cool :)
        console.log(currentNode.data);

        currentChildren = currentNode.children;
        // id there are any children in the node 
        // add them at the end of the queue 
        if (currentChildren !== null) {
            for (const child of currentChildren) {
                queue.push(child);
            }
        }
    }
}