Walking a tree (depth first search)

Intro

A short blog on how you can traverse a tree in depth. Depth first search is a an algorithm that goes as deep as it can
(it is easier to see what "deep" means in an example)

depth first search

First, imagine a tree not as a regular tree, but as an a upside down tree (I was really confused about it, because the root is on the top and not at the bottom).

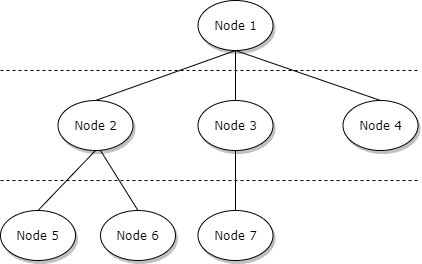
Let's take for example the following tree:

The idea is to traverse the tree as deep as you can first, and if you cannot go deeper, then you can visit the next sibling and deep again.

Let's see how dfs (depth first search) works in the above tree:

1. visit node ''node 1'', now ''node 1'' has three children, ''node 4'', ''node 3'' and ''node 2''
2. visit ''node 4''
3. ''node 4'' has no children, so we cannot go deeper
4. visit ''node 3'', now ''node 3'' has a child, ''node 7''
5. visit ''node 7''
6. ''node 7'' has no children, so we cannot go deeper
7. visit ''node 2'', now ''node 2'' has two children, ''node 6'' and ''node 5''
8. visit ''node 5''
9. ''node 5'' has no children, so we cannot go deeper
10. visit ''node 6''
11. ''node 6'' has no children, so we cannot go deeper

js implementation

What is needed for a depth first implementation in a tree:

1. a stack
2. a tree

the algorithm in plain english:

1. initialize an empty stack
2. take the root from the tree
3. add it to the top of the stack
4. while there are nodes in the stack do:
5.      take/remove the first element from the top of the stack
6.      process the data of the current node
7.      if current node has any children add them to the top of the stack

the algorithm in js:

// a tree node looks like this
rootNode = {
    id: 1,
    data: 1,
    children: [secondNode, thirdNode, forthNode]
};


function depthFirstSearch(rootNode) {
    let stack = [];
    stack.push(rootNode);

    while (stack.length !== 0) {
        // remove the first child in the stack
        currentNode = stack.splice(-1, 1)[0];
        // do something cool with the data
        // printing them is also cool :)
        console.log(currentNode.id);

        currentChildren = currentNode.children;
        // is there are any children in the node
        // add them at the top of the stack
        if (currentChildren !== null) {
            for (let index = 0; index < currentChildren.length; index++) {
                const child = currentChildren[index];
                stack.push(child);
            }
        }
    }
}

Comments

[Konstantinos Blatsoukas]

Hi Nam,

Thanks for the comment!

• in the bfs implementation you need to utilize a queue and a tree (see my previous article dev.to/konstantinosblatsoukasrepo/...)

• there will be a need to mark the visited nodes in case of graph (in order to avoid cycles). In a tree, you don't have that problem (there is no cycle)

• if that was a bfs the nodes will be traversed layer by layer, in the above code that doesn't happens

• now, a stack is a data structure that is like a stack of plates, possible operatios:

1. Put something in the top of a stack
2. Remove something from the top

In this case, I used a js array as a stack, I was adding something at the end of the array and removing something from the end of the array

[Konstantinos Blatsoukas]

Yes you are right I have not explained the tree object, I will do that! Thanks!

[Nam Hoang Le]

Oops, I’m wrong at some points. Btw, thanks for sharing.
Cheers.

[Konstantinos Blatsoukas]

Nam, I just added how a tree node looks like! thanks again for your comment

[Nam Hoang Le]

That is a ideal structure, and does not exist in reality world. I believe that we will have adjacency list only.

[Nam Hoang Le]

First, if you need to introduce data structure of a problem. What is the children of the node? What is the stack?
Next, I believe you need to object (or array) to mark visited nodes.
But in general, I think you are implementing an breadth first search (BFS) algorithm.
Please feedback if I’m wrong.