Problem Description
The task of the problem at hand is quite clear: implement an exponentiation function, pow(x, n), that raises x to the power of n (n is an integer). Original link here.
Constraints:
- -100.0 < x < 100.0
- -2^31 <= n <= 2^31-1
- -10^4 <= x^n <= 10^4
Example 1:
- input: x = 2.10000, n = 3
- output: 9.26100
Example 2:
- input: x = 2.00000, n = -2
- output: 0.25000
Let's talk about solutions
It is obvious that we can of course multiply the number x by itself n times (and in the case of n being negative, multiply 1/x by itself the corresponding number of times). This approach takes O(n) time and is not the fastest one.
The optimal approach is obtained by making a simple statement:
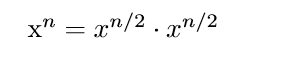
And then:
We can then calculate x to the power of n by calculating x^2, then x^4 (by multiplying x^2 by itself) and so forth, until we get to x^n.
The algorithm looks like this:
- if n is negative, we make x equal 1/x and n equal -n and take a dump variable, a to equal 1; a will help us later.
- as long as n is greater than 0:
- if we find an odd n, we multiply a by x.
- we multiply x by itself and store the result in x.
- we divide n by 2 and store the result in n.
- when n becomes 0, the result will be in a, because there will always be a case when n will be odd; the motivation for this can come from the prime factorisation of an arbitrary number - 2 is the only even prime factor, and if we continue to divide by it we will get to a point at which there will be no 2s left in the prime factorisation of the number.
For this approach to factorisation, we have to perform log n operations. If n doubles, then the operations performed only grow by 1, as opposed to the first approach, in which the number of operations performed will double if n doubles.
This is a very basic implementation of the algorithm:
This approach is called logarithmic exponentiation and an examples where it proves useful is computing recurrence relations. I provided a more detailed description of the matter in this article I wrote some time ago, which explains how to compute Fibonacci numbers using fast matrix exponentiation.
That concludes today's solution. I'll be back with other LeetCode solutions (including harder ones!) for the LeetCode Explained series, so don't forget to subscribe!


Top comments (0)