During the previous articles in the series, we have explored some properties of the very famous Fibonacci series. Today, we are going to speak about the golden ratio and present two extremely interesting methods of computing the n-th Fibonacci number.
Golden ratio
You may have heard about this concept before. In mathematics, 2 quantities are in the golden ratio if their ratio is equal to the ratio between the sum and the larger of the quantities. It is also defined as the positive solution of the following quadratic equation:
It is represented by the greek letter phi. When solving the equation, we get:
It appears throughout many natural, architectural and mathematical settings and you can read more about it here.
Why is it related to the Fibonacci numbers, though? Well, suppose we have some number n. When n tends to get larger and larger, the ratio between the n+1-st Fibonacci number and the n-th is approximately equal to the golden ratio. From a mathematical perspective:
Now, let's try and solve the recurrence relation of the Fibonacci series. For that, I'm going to use the characteristic polynomial of the recurrence relation the defines the Fibonacci numbers (if you are not familiar with solving those relations, this page offers some great insight on how this works)
The Fibonacci numbers are defined by the following relation:
When plugging those number in its characteristic polynomial, we get:
Looks familiar? The solution of this equation is phi and its conjugate (minus the square root instead of plus)
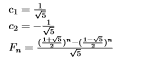
Now, the n-th Fibonacci number is defined by the following:
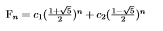
And upon solving the 2 equations resulted from F0 and F1, we get:
Computing the approximate of the n-th Fibonacci number using the closed formula
The closed formula above quickly leads us to another way of computing the Fibonacci numbers: using the formula directly. However, this method has 2 possible time complexities:
- O(n), if we raise the 2 numbers to the n-th power in linear time, using the basic algorithm.
- O(log n), if we use exponentiation by squaring.
However, because of the way that irrational numbers are stored in memory (as approximates), the first approach will be a lot less efficient than the direct iterative method presented in the previous post.
Either one of these methods would only provide approximates, though.
Here's a snippet of code for the second method:
long double lgPow(long double x, int p) { /// computing x^p in logarithmic time
long double ans = 1;
while(p > 0) {
while(p%2 == 0) {
x = x*x;
p /= 2;
}
ans = ans*x;
p--;
}
return ans;
}
long double approxFibo(int n) {
long double phi = (1 + sqrt(5)) / 2,
psi = (1 - sqrt(5)) / 2;
return (lgPow(phi, n) - lgPow(psi, n)) / sqrt(5);
}
Computing the n-th Fibonacci number in O(log n) time and constant space
A very efficient way to compute the n-th Fibonacci number is through using matrix multiplication.
Suppose that we have the k and k+1-st Fibonacci numbers already calculated in a matrix. We will need a matrix with which to multiply the current one so that instead of the k-th number we will have the k+1-st and instead of the k+1-st we will have the k+2-nd. One way of doing that is this:
We can use this approach to rapidly compute the n-th Fibonacci number, in O(n) time. The trick is to raise the first matrix on the right hand side to the n-2nd power in logarithmic time. Below you can see a concrete code example. For code readability and in order to keep the logarithmic time exponentiation similar to the previous one, I've chosen to create a matrix class and overload some operators.
int zeroM[2][2] = {{0, 0}, {0, 0}},
idenM[2][2] = {{1, 0}, {1, 0}};
class matrix {
private: int v[2][2]; /// we only need a 2x2 matrix for the job
public:
matrix(int x[][2] = zeroM) {
for(int i = 0; i < 2; i++)
for(int j = 0; j < 2; j++)
v[i][j] = x[i][j];
}
int element(int x, int y) {
return v[x][y];
}
friend matrix operator*(const matrix& A, const matrix& B) {
matrix R;
for(int i = 0; i < 2; i++)
for(int j = 0; j < 2; j++)
for(int k = 0; k < 2; k++)
R.v[i][j] += A.v[i][k] * B.v[k][j];
return R;
}
friend matrix operator^(matrix X, int p) { /// computing X^p in logarithmic time
matrix R(idenM); /// intialising R as the identity matrix
while(p > 0) {
while(p%2 == 0) {
X = X * X;
p /= 2;
}
R = X * R;
p--;
}
return R;
}
};
int logFibo(int n) {
int xM[2][2] = {{1, 1}, {1, 0}},
fM[2][2] = {{1, 0}, {1, 0}};
matrix X(xM),
F(fM);
X = X^(n-2);
F = F * X;
return F.element(0, 0);
}
This approach is extremely useful when dealing with recurrence relations / dynamic programming problems as it can be used to dramatically reduce the time complexity of computing a recurrence relation (from O(n) to O(log n)).
Well, it seems that our Fibonacci-related articles have come to an end. Do you think that we managed to answer the question we posed in the first article? I think yes. People love the Fibonacci numbers because they are a fairly easy concept which can teach us a lot of things about computer science: weighing the advantages and disadvantages of recursion, memoization, matrix multiplication, exponentiation by squaring, all of which can be used in various context to increase runtime. They also have a lot more interesting properties than what I have managed to present during the last 3 articles. In the end, they are truly magical.
I will continue "The Magic of Computing" with lots of other computer science articles, covering various topics, algorithms and data structures as well as try to integrate them in the "real world". What did you think about these 3 Fibonacci articles? Is there something you wish me to write about next? Please, let me know below!

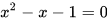
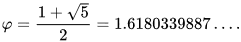
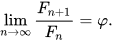

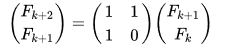

Top comments (0)