In the previous article, I wrote about Binary Search Tree and saw if I could implement it to my Chrome Extension. A simple binary search tree was not perfect for my project, however, I discovered that some of the features within the tree structure is useful for the project.
Currently, I'm storing the main data as objects in an array like this:
// Result of console.log(main-data)
(4)[{...}, {...}, {...}, {...}]
0: {category: "cat1", id: "4", meaning: "information of the vocabulary.", tag: ["tag1", "tag2"], word: "Example Vocab 1"}
1: {category: "cat3", id: "3", meaning: "Hello World", tag: ["tag1", "tag4"], word: "Example Vocab 2"}
2: {category: "cat2", id: "2", meaning: "This is new vocabulary.", tag: ["tag4"], word: "Example"}
3: {category: "cat4", id: "1", meaning: "You can write anything.", tag: ["tag2", "tag4", "tag5"], word: "Sample"}
In this situation, insertion and deletion take O(n). Therefore I'm still looking for a data structure that is hopefully O(1).
What I learned after the Binary search tree was Binary Heaps. In this article, I'm going to think about if it can be suitable or not.
What is Binary Heap?
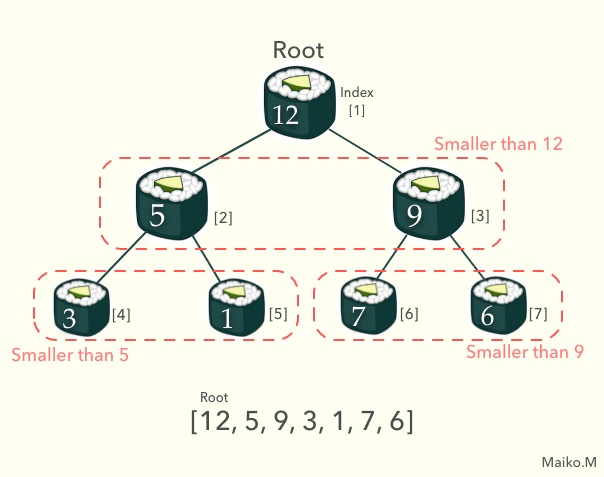
Heap is one of the categories within the tree data type, and Binary Heap is categorized into heaps. A binary heap takes the form of binary tree.
We can implement it with an Array so that each value will have an index.
And same as Binary Search Tree, each value has 0 to 2 children, but not more than 2.
When a binary heap is a Max Binary Heap, parent nodes are always larger than children nodes. When a binary heap is a Min Binary Heap, parent nodes are always smaller than child nodes.
These features make binary heaps good at finding the max number, and also keep update the list when removing the max number or inserting a new number.
Removing the max number
When we remove the largest number in the array, we want to find out which one will be the next largest number. We could probably see one of the children nodes and directly place it as the largest number, but that makes the rest of the order messed up.
To place the next largest number at the beginning of the list, and not to mess up the list either, we can implement bubble-down method. Firstly place the last number in the Array to the beginning of the list, and we can sink down the number until it finds the correct spot.
Bubble down steps
We only need a few steps to sort the array.
(1) Take the last number in the Array (We will call it target here), and place it at the root.
(2) Compare the target and its children.
- If one of them is larger than the target, swap the target and the larger child.
- If both of them are larger than the target, swap target and the largest child.
- If both children are smaller than the target, that'll be the correct spot.
Inserting a number
When we add a new random number into the array, we can implement bubble-up method to find out its correct spot, and keep the entire array sorted as it should be.
Bubble-up steps
It is just opposite the bubble-down method.
(1) Firstly, insert the new number at the end of the array.
(2) Compare the target number and its parent.
- If the parent number is smaller than the target, swap each other.
- If the parent number is larger than the target, then it's in the correct spot.
Basic Implementation
We'll implement it as an Array, so we only need to initialize MaxBinaryHeap class.
class MaxBinaryHeap {
constructor() {
this.heap = [];
}
}
Remove Max Implementation
It takes time complexity of O(log n) when we use a bubble-down method.
removeMax() {
let removed = this.heap[0];
let end = this.heap.pop();
if (this.heap.length > 0) {
this.heap[0] = end;
this.bubbleDown();
}
return removed;
}
Bubble Down Implementation
bubbleDown() {
let targetIdx = 0;
while (true) {
let target = this.heap[targetIdx];
let leftChildIdx = targetIdx * 2 + 1;
let rightChildIdx = targetIdx * 2 + 2;
let left = this.heap[leftChildIdx];
let right = this.heap[rightChildIdx];
let swap = null;
if (leftChildIdx < this.heap.length && target < left){
swap = leftChildIdx;
}
if (rightChildIdx < this.heap.length && target < right && left < right){
swap = rightChildIdx;
}
if (swap === null) break;
this.heap[targetIdx] = this.heap[swap];
this.heap[swap] = target;
targetIdx = swap;
}
}
Insertion Implementation
Insertion is also O(log n) with bubble-up method.
insert(val) {
this.heap.push(val);
this.bubbleUp();
}
Bubble-up Implementation
bubbleUp() {
let targetIdx = this.heap.length - 1;
let target = this.heap[targetIdx]
while(targetIdx > 0){
let parentIdx = Math.floor((targetIdx - 1) / 2);
let parent = this.heap[parentIdx]
if (target > parent) {
this.heap[parentIdx] = target;
this.heap[targetIdx] = parent;
targetIdx = parentIdx;
}
if (target <= parent) break;
}
}
Conclusion
Priority queues can be efficiently implemented using Binary Heap, but in my Chrome Extension, there is no priority and it needs to be also efficient when we remove an element in the middle of the list.
We won't implement Binary Heap this time, but the Heap data structure itself is enormously used, thus it's definitely worth practicing it.
Reference
JavaScript Algorithms and Data Structures Masterclass (Udemy)
List of data structures (Wikipedia)





Top comments (2)
Thanks for the reference.
You are welcome! :)