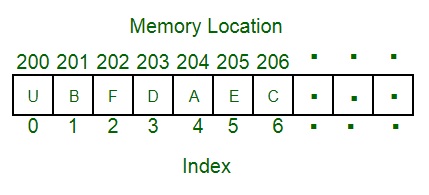
Data Structures basically describes how we can ogarnise and stored in memory when a program processes it.For example, we can store a list of items having the same data-type using the array data structure.
An Algorithm on the other hand, is step by step set of instruction to process the data for a specific purpose. So, an algorithm uterlises various data structures in a logical way to solve a specific computing problem.This is a very important concept in computer science .It gives us more insight on the data we are working with.It enables data scientists to make better machine learning predictions.This is however a challenging topic to most people in the tech industry , according to most people.We are going to look at various python data structures in python and their code examples.
Lists
The list is a most versatile datatype available in Python which can be written as a list of comma-separated values (items) between square brackets.Lists are mutable and ordered. It can contain a mix of different data types.
list1 = ['chicken', 'pizza', 2022, 2000]
list2 = [1, 2, 3, 4, 5 ]
list3 = ["a", "b", "c", "d"]
We can access values in a list using their index.
NOTE: we start counting from 0
print (list1[0]) #prints the element in the 0 index
We also use the .append() method to add new items into the list eg
list2.append(6) #add 6 to the existing list2
Incase you want to add to a specific place in the list ,we do it as follows
list3[2] = "e" # returns ["a", "b", "e", "d"]
Some basic list operations include:
- len([1, 2, 3]) resulting to 3 which tests the Length
- [1, 2, 3] + [4, 5, 6]resulting to[1, 2, 3, 4, 5, 6]|Concatenation
- ['Hi!'] * 3 resulting to ['Hi!', 'Hi!', 'Hi!'] which tests Repetition
- 3 in [1, 2, 3] resulting to True which tests Membership
- for x in [1, 2, 3]:print x resulting to 1 2 3 which tests Iteration
Dictionaries
Dictionary is a mutable and unordered data structure. It permits storing a pair of items (i.e. keys and values).Each key is separated from its value by a colon (:), the items are separated by commas, and the whole thing is enclosed in curly braces. An empty dictionary without any items is written with just two curly braces, like this − {}.
Keys are unique within a dictionary while values may not be. The values of a dictionary can be of any type, but the keys must be of an immutable data type such as strings, numbers, or tuples.
Accessing Values in Dictionary
To access dictionary elements, you can use the familiar square brackets along with the key to obtain its value.
Example:
dict = {'Name': 'Marrie', 'Age': 27, 'Language': 'Python'}
print "dict['Name']: ", dict['Name']
print "dict['Age']: ", dict['Age']
When the above code is executed, it produces the following result :
dict['Name']: Marrie
dict['Age']: 27
If we attempt to access a data item with a key, which is not part of the dictionary, we get an error as follows:
Example
#Using the data above.
print "dict['Alice']: ", dict['Alice']
When the above code is executed, it produces the following result :
dict['Alice']:
Traceback (most recent call last):
File "test.py", line 4, in <module>
print "dict['Alice']: ", dict['Alice'];
KeyError: 'Alice'
Updating Dictionary
You can update a dictionary by adding a new entry or a key-value pair, modifying an existing entry, or deleting an existing entry as shown below in the simple example:
dict = {'Name': 'Marrie', 'Age': 27, 'Language': 'Python'}
dict['Age'] = 28; # update existing entry
dict['School'] = "LuxAcademy"; # Add new entry
print "dict['Age']: ", dict['Age']
print "dict['School']: ", dict['School']
When the above code is executed, it produces the following result :
dict['Age']: 28
dict['School']:LuxTech
Delete Dictionary Elements
You can either remove individual dictionary elements or clear the entire contents of a dictionary. You can also delete entire dictionary in a single operation.
To explicitly remove an entire dictionary, just use the del statement.
dict = {'Name': 'Marrie', 'Age': 27, 'Language': 'Python'}
del dict['Name']; # remove entry with key 'Name'
dict.clear(); # remove all entries in dict
del dict ; # delete entire dictionary
print "dict['Age']: ", dict['Age']
print "dict['School']: ", dict['School']
Note −that an exception is raised because after del dict dictionary does not exist any more:
dict['Age']:
Traceback (most recent call last):
File "test.py", line 8, in <module>
print "dict['Age']: ", dict['Age'];
TypeError: 'type' object is unsubscriptable
Properties of Dictionary Keys
Dictionary values have no restrictions. They can be any arbitrary Python object, either standard objects or user-defined objects. However, same is not true for the keys.
There are two important points to remember about dictionary keys:
*More than one entry per key not allowed. Which means no duplicate key is allowed. When duplicate keys encountered during assignment, the last assignment wins.
dict = {'Name': 'Marrie', 'Age': 27, 'Name': 'Python'}
print "dict['Name']: ", dict['Name']
When the above code is executed, it produces the following result:
dict['Name']: Python
*Keys must be immutable. Which means you can use strings, numbers or tuples as dictionary keys but something like ['key'] is not allowed.
An example is as follows :
dict = {['Name']: 'Marrie', 'Age': 27}
print "dict['Name']: ", dict['Name']
When the above code is executed, it produces the following result :
Traceback (most recent call last):
File "test.py", line 3, in <module>
dict = {['Name']: 'Marrie', 'Age': 27};
TypeError: list objects are unhashable
Tuples
A tuple is another container. It is a data type for immutable ordered sequences of elements. Immutable because you can’t add and remove elements from tuples, or sort them in place.
Creating a tuple is as simple as putting different comma-separated values. Optionally you can put these comma-separated values between parentheses also.
For example:
tuple_one = ('python', 'javascript', 'c++', 2000);
tuple_two = (1, 2, 3, 4, 5 );
tuple_3 = "a", "b", "c", "d";
The empty tuple is written as two parentheses containing nothing −
languages = ();
To write a tuple containing a single value you have to include a comma, even though there is only one value −
tup1 = (50,);
Like string indices, tuple indices start at 0, and they can be sliced, concatenated, and so on.
Accessing Values in Tuples
To access values in tuple, use the square brackets for slicing along with the index or indices to obtain value available at that index.
For example
tuple_one = ('python', 'javascript', 'c++', 2000);
tuple_two = (1, 2, 3, 4, 5 );
print "tuple_one[0]: ", tuple_two[0];
print "tuple_two[1:5]: ",tuple_two[1:5];
When the above code is executed, it produces the following result :
tuple_one[0]: python
tuple_two[1:5]: [2, 3, 4, 5]
Updating Tuples
Tuples are immutable which means you cannot update or change the values of tuple elements. You are able to take portions of existing tuples to create new tuples as the following example demonstrates −
tup1 = (12, 34.56);
tup2 = ('abc', 'xyz');
# Following action is not valid for tuples
# tup1[0] = 100;
# So let's create a new tuple as follows
tup3 = tup1 + tup2;
print tup3;
When the above code is executed, it produces the following result:
(12, 34.56, 'abc', 'xyz')
Delete Tuple Elements
Removing individual tuple elements is not possible. There is, of course, nothing wrong with putting together another tuple with the undesired elements discarded.
To explicitly remove an entire tuple, just use the del statement.
For example:
tuple_one = ('python', 'javascript', 'c++', 2000);
print tuple_one;
del tuple_one;
print "After deleting tup : ";
print tuple_one;
Note − an exception raised, this is because after del tup tuple does not exist anymore.
This produces the following result:
('python', 'javascript', 'c++', 2000)
After deleting tup :
Traceback (most recent call last):
File "test.py", line 9, in <module>
print tuple_one;
NameError: name 'tuple_one' is not defined.
Assuming our file name is "test.py"
Basic Tuples Operations
Tuples respond to the + and * operators much like strings; they mean concatenation and repetition here too, except that the result is a new tuple, not a string.
In fact, tuples respond to all of the general sequence operations we used on strings in the prior chapter.
- len((1, 2, 3)) which results to 3 used to test Length
- (1, 2, 3) + (4, 5, 6)which results to(1, 2, 3, 4, 5,6) and is used to test Concatenation
- ('Hi!',) * 4 which results to('Hi!', 'Hi!', 'Hi!', 'Hi!') and is used to test Repetition
- 3 in (1, 2, 3) which results to True and is used to test Membership
- for x in (1, 2, 3): print x which results to 1 2 3 and is used to test Iteration
Sets
Set is a mutable and unordered collection of unique elements. It can permit us to remove duplicate quickly from a list.The sets in python are typically used for mathematical operations like union, intersection, difference and complement etc.
A Python set is similar to this mathematical definition with below additional conditions:
*The elements in the set cannot be duplicates.
*The elements in the set are immutable(cannot be modified) but the set as a whole is mutable.
*There is no index attached to any element in a python set. So they do not support any indexing or slicing operation.Creating a set
A set is created by using the set() function or placing all the elements within a pair of curly braces.
Days=set(["Mon","Tue","Wed","Thu","Fri","Sat","Sun"])
Months={"Jan","Feb","Mar"}
Dates={21,22,17}
print(Days)
print(Months)
print(Dates)
Note how the order of the elements has changed in the result.
set(['Wed', 'Sun', 'Fri', 'Tue', 'Mon', 'Thu', 'Sat'])
set(['Jan', 'Mar', 'Feb'])
set([17, 21, 22])
Accessing Values in a Set
We cannot access individual values in a set. We can only access all the elements together as shown above. But we can also get a list of individual elements by looping through the set.
#Considering the data above.
Days=set(["Mon","Tue","Wed","Thu","Fri","Sat","Sun"])
for d in Days:
print(d)
When the above code is executed, it produces the following :
Wed
Sun
Fri
Tue
Mon
Thu
Sat
Adding Items to a Set
We can add elements to a set by using add() method. Remember,there is no specific index attached to the newly added element.
#Adding to the data above.
Days.add("Sun")
print(Days)
results
set(['Wed', 'Sun', 'Fri', 'Tue', 'Mon', 'Thu', 'Sat'])
Removing Item from a Set
We can remove elements from a set by using discard() method.
Example
#Using the data above.
Days.discard("Sun")
print(Days)
Output
set(['Wed', 'Fri', 'Tue', 'Mon', 'Thu', 'Sat'])
Union of Sets
The union operation on two sets produces a new set containing all the distinct elements from both the sets. In the below example the element “Wed” is present in both the sets.
DaysA = set(["Mon","Tue","Wed"])
DaysB = set(["Wed","Thu","Fri","Sat","Sun"])
AllDays = DaysA|DaysB
print(AllDays)
Output will be as shown,note the result has only one “wed”.
set(['Wed', 'Fri', 'Tue', 'Mon', 'Thu', 'Sat'])
Intersection of Sets
The intersection operation on two sets produces a new set containing only the common elements from both the sets. In the below example the element “Wed” is present in both the sets.
DaysA = set(["Mon","Tue","Wed"])
DaysB = set(["Wed","Thu","Fri","Sat","Sun"])
AllDays = DaysA & DaysB
print(AllDays)
Output
set(['Wed'])
Difference of Sets
The difference operation on two sets produces a new set containing only the elements from the first set and none from the second set. In the below example the element “Wed” is present in both the sets so it will not be found in the result set.
DaysA = set(["Mon","Tue","Wed"])
DaysB = set(["Wed","Thu","Fri","Sat","Sun"])
AllDays = DaysA - DaysB
print(AllDays)
Output
When the above code is executed, it produces the following result. Please note the result has only one “wed”.
set(['Mon', 'Tue'])
Compare Sets
We can check if a given set is a subset or superset of another set. The result is True or False depending on the elements present in the sets.
Example
DaysA = set(["Mon","Tue","Wed"])
DaysB = set(["Mon","Tue","Wed","Thu","Fri","Sat","Sun"])
SubsetRes = DaysA <= DaysB
SupersetRes = DaysB >= DaysA
print(SubsetRes)
print(SupersetRes)
Output
True
True
Queue
The queue is a linear data structure where elements are in a sequential manner. It follows the F.I.F.O mechanism that means first in first out.
Below the aspects that characterize a queue.
Two ends:
*front → points to starting element
*rear → points to the last element
There are two operations:
*enqueue → inserting an element into the queue. It will be done at the rear.
*dequeue → deleting an element from the queue. It will be done at the front.
There are two conditions:
*overflow → insertion into a queue that is full
*underflow → deletion from the empty queue
Lets see a code example of this:
class myqueue:
def __init__(self):
self.data = []
def length(self):
return len(self.data)
def enque(self, element): # put the element in the queue
if len(self.data) < 5:
return self.data.append(element)
else:
return "overflow"
def deque(self): # remove the first element that we have put in queue
if len(self.data) == 0:
return "underflow"
else:
self.data.pop(0)
b = myqueue()
b.enque(2) # put the element into the queue
b.enque(3)
b.enque(4)
b.enque(5)
print(b.data)
b.deque()# # remove the first element that we have put in the queue
print(b.data)
This will procuce the following results.
[2, 3, 4, 5]
[3, 4, 5]
Stack
In the english dictionary the word stack means arranging objects on over another. Stack is a linear data structure which follows a particular order in which the operations are performed. The order may be LIFO(Last In First Out) or FILO(First In Last Out).
In the following program we implement it as add and and remove functions. We declare an empty list and use the append() and pop() methods to add and remove the data elements.
Pushing into a Stack
Example
class Stack:
def __init__(self):
self.stack = []
def add(self, dataval):
# Use list append method to add element
if dataval not in self.stack:
self.stack.append(dataval)
return True
else:
return False
# Use peek to look at the top of the stack
def peek(self):
return self.stack[-1]
AStack = Stack()
AStack.add("Mon")
AStack.add("Tue")
AStack.peek()
print(AStack.peek())
AStack.add("Wed")
AStack.add("Thu")
print(AStack.peek())
Output
Tue
Thu
POP from a Stack
As we know we can remove only the top most data element from the stack, we implement a python program which does that. The remove function in the following program returns the top most element. We check the top element by calculating the size of the stack first and then use the in-built pop() method to find out the top most element.
class Stack:
def __init__(self):
self.stack = []
def add(self, dataval):
# Use list append method to add element
if dataval not in self.stack:
self.stack.append(dataval)
return True
else:
return False
# Use list pop method to remove element
def remove(self):
if len(self.stack) <= 0:
return ("No element in the Stack")
else:
return self.stack.pop()
AStack = Stack()
AStack.add("Mon")
AStack.add("Tue")
AStack.add("Wed")
AStack.add("Thu")
print(AStack.remove())
print(AStack.remove())
Output:
Thu
Wed
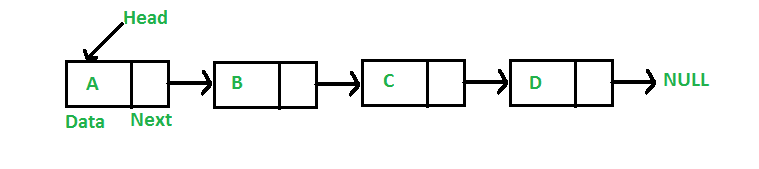
Linked list
A linked list is a linear data structure, in which the elements are not stored at contiguous memory locations. The elements in a linked list are linked using pointers as shown in the below image:
Now lets create a linked list
class Node:
def __init__(self, dataval=None):
self.dataval = dataval
self.nextval = None
class SLinkedList:
def __init__(self):
self.headval = None
list1 = SLinkedList()
list1.headval = Node("Mon")
e2 = Node("Tue")
e3 = Node("Wed")
# Link first Node to second node
list1.headval.nextval = e2
# Link second Node to third node
e2.nextval = e3
Traversing a Linked List
Singly linked lists can be traversed in only forward direction starting form the first data element. We simply print the value of the next data element by assigning the pointer of the next node to the current data element.
Example
class Node:
def __init__(self, dataval=None):
self.dataval = dataval
self.nextval = None
class SLinkedList:
def __init__(self):
self.headval = None
def listprint(self):
printval = self.headval
while printval is not None:
print (printval.dataval)
printval = printval.nextval
list = SLinkedList()
list.headval = Node("Mon")
e2 = Node("Tue")
e3 = Node("Wed")
# Link first Node to second node
list.headval.nextval = e2
# Link second Node to third node
e2.nextval = e3
list.listprint()
Output:
Mon
Tue
Wed
Insertion in a Linked List
Inserting element in the linked list involves reassigning the pointers from the existing nodes to the newly inserted node. Depending on whether the new data element is getting inserted at the beginning or at the middle or at the end of the linked list, we have the below scenarios.
Inserting at the Beginning
This involves pointing the next pointer of the new data node to the current head of the linked list. So the current head of the linked list becomes the second data element and the new node becomes the head of the linked list.
Example
class Node:
def __init__(self, dataval=None):
self.dataval = dataval
self.nextval = None
class SLinkedList:
def __init__(self):
self.headval = None
# Print the linked list
def listprint(self):
printval = self.headval
while printval is not None:
print (printval.dataval)
printval = printval.nextval
def AtBegining(self,newdata):
NewNode = Node(newdata)
# Update the new nodes next val to existing node
NewNode.nextval = self.headval
self.headval = NewNode
list = SLinkedList()
list.headval = Node("Mon")
e2 = Node("Tue")
e3 = Node("Wed")
list.headval.nextval = e2
e2.nextval = e3
list.AtBegining("Sun")
list.listprint()
Output:
Sun
Mon
Tue
Wed
Inserting at the End
This involves pointing the next pointer of the the current last node of the linked list to the new data node. So the current last node of the linked list becomes the second last data node and the new node becomes the last node of the linked list.
Example
class Node:
def __init__(self, dataval=None):
self.dataval = dataval
self.nextval = None
class SLinkedList:
def __init__(self):
self.headval = None
# Function to add newnode
def AtEnd(self, newdata):
NewNode = Node(newdata)
if self.headval is None:
self.headval = NewNode
return
laste = self.headval
while(laste.nextval):
laste = laste.nextval
laste.nextval=NewNode
# Print the linked list
def listprint(self):
printval = self.headval
while printval is not None:
print (printval.dataval)
printval = printval.nextval
list = SLinkedList()
list.headval = Node("Mon")
e2 = Node("Tue")
e3 = Node("Wed")
list.headval.nextval = e2
e2.nextval = e3
list.AtEnd("Thu")
list.listprint()
Output
Mon
Tue
Wed
Thu
Inserting in between two Data Nodes
This involves changing the pointer of a specific node to point to the new node. That is possible by passing in both the new node and the existing node after which the new node will be inserted. So we define an additional class which will change the next pointer of the new node to the next pointer of middle node. Then assign the new node to next pointer of the middle node.
class Node:
def __init__(self, dataval=None):
self.dataval = dataval
self.nextval = None
class SLinkedList:
def __init__(self):
self.headval = None
# Function to add node
def Inbetween(self,middle_node,newdata):
if middle_node is None:
print("The mentioned node is absent")
return
NewNode = Node(newdata)
NewNode.nextval = middle_node.nextval
middle_node.nextval = NewNode
# Print the linked list
def listprint(self):
printval = self.headval
while printval is not None:
print (printval.dataval)
printval = printval.nextval
list = SLinkedList()
list.headval = Node("Mon")
e2 = Node("Tue")
e3 = Node("Thu")
list.headval.nextval = e2
e2.nextval = e3
list.Inbetween(list.headval.nextval,"Fri")
list.listprint()
Output:
Mon
Tue
Fri
Thu
Removing an Item
We can remove an existing node using the key for that node. In the below program we locate the previous node of the node which is to be deleted.Then, point the next pointer of this node to the next node of the node to be deleted.
Example
class Node:
def __init__(self, data=None):
self.data = data
self.next = None
class SLinkedList:
def __init__(self):
self.head = None
def Atbegining(self, data_in):
NewNode = Node(data_in)
NewNode.next = self.head
self.head = NewNode
# Function to remove node
def RemoveNode(self, Removekey):
HeadVal = self.head
if (HeadVal is not None):
if (HeadVal.data == Removekey):
self.head = HeadVal.next
HeadVal = None
return
while (HeadVal is not None):
if HeadVal.data == Removekey:
break
prev = HeadVal
HeadVal = HeadVal.next
if (HeadVal == None):
return
prev.next = HeadVal.next
HeadVal = None
def LListprint(self):
printval = self.head
while (printval):
print(printval.data),
printval = printval.next
llist = SLinkedList()
llist.Atbegining("Mon")
llist.Atbegining("Tue")
llist.Atbegining("Wed")
llist.Atbegining("Thu")
llist.RemoveNode("Tue")
llist.LListprint()
Output:
Thu
Wed
Mon
Algorithims
Algorithms are instructions that are formulated in a finite and sequential order to solve problems.
The word algorithm derives itself from the 9th-century Persian mathematician Muḥammad ibn Mūsā al-Khwārizmī, whose name was Latinized as Algorithmi. Al-Khwārizmī was also an astronomer, geographer, and a scholar in the House of Wisdom in Baghdad.
As you already know algorithms are instructions that are formulated in a finite and sequential order to solve problems.
When we write an algorithm, we have to know what is the exact problem, determine where we need to start and stop and formulate the intermediate steps.
There are three main approaches to solve algorithms:
*Divide et Impera (also known as divide and conquer) → it divides the problem into sub-parts and solves each one separately
*Dynamic programming → it divides the problem into sub-parts remembers the results of the sub-parts and applies it to similar ones
*Greedy algorithms → involve taking the easiest step while solving a problem without worrying about the complexity of the future steps
Tree Traversal Algorithm
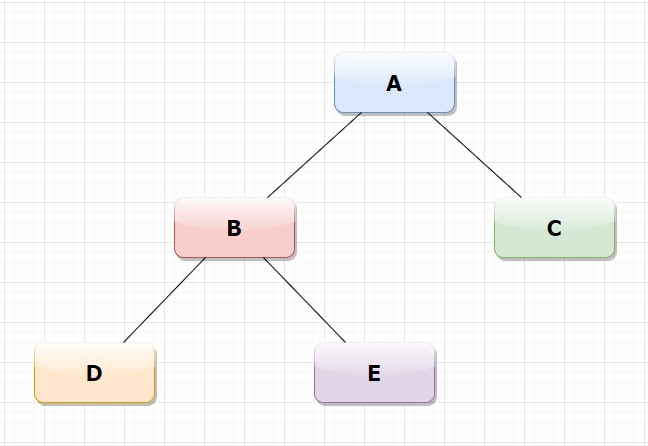
Trees in python are non-linear data structures. They are characterized by roots and nodes. I take the class I constructed before for the binary tree.
Tree Traversal refers to visiting each node present in the tree exactly once, in order to update or check them.
# create the class Node and the attrbutes
class Node:
def __init__(self, letter):
self.childleft = None
self.childright = None
self.nodedata = letter
# create the nodes for the tree
root = Node('A')
root.childleft = Node('B')
root.childright = Node('C')
root.childleft.childleft = Node('D')
root.childleft.childright = Node('E')
There are three types of tree traversals:
*In-order traversal → refers to visiting the left node, followed by the root and then the right nodes.
Here D is the leftmost node where the nearest root is B. The right of root B is E. Now the left sub-tree is completed, so I move towards the root node A and then to node C.
def InOrd(root):
if root:
InOrd(root.childleft)
print(root.nodedata)
InOrd(root.childright)
InOrd(root)
Out:
D
B
E
A
C
*Pre-order traversal → refers to visiting the root node followed by the left nodes and then the right nodes.
In this case, I move to the root node A and then to the left child node B and to the sub child node D. After that I can go to the nodes E and then C.
def PreOrd(root):
if root:
print(root.nodedata)
PreOrd(root.childleft)
PreOrd(root.childright)
PreOrd(root)
out:
A
B
D
E
C
*Post-order traversal → refers to visiting the left nodes followed by the right nodes and then the root node.
I go to the most left node which is D and then to the right node E. Then, I can go from the left node B to the right node C. Finally, I move towards the root node A.
def PostOrd(root):
if root:
PostOrd(root.childleft)
PostOrd(root.childright)
print(root.nodedata)
PostOrd(root)
out:
D
E
B
C
A
Sorting Algorithm
The sorting algorithm is used to sort data in some given order. It can be classified in Merge Sort and Bubble Sort.
*Merge Sort → it follows the divide et Impera rule. The given list is first divided into smaller lists and compares adjacent lists and then, reorders them in the desired sequence. So, in summary from unordered elements as input, we need to have ordered elements as output. Below, the code with each step described.
def merge_sort(ourlist, left, right): #left and right corresponds to starting and ending element of ourlist
if right -left > 1: # check if the length of ourlist is greater than 1
middle = (left + right) // 2 # we divide the length in two parts
merge_sort(ourlist, left, middle) # recursevely I call the merge_sort function from left to middle
merge_sort(ourlist, middle, right) # then from middle to right
merge_list(ourlist, left, middle, right) # finally I create ourlist in complete form(left, middle and right)
def merge_list(ourlist, left, middle, right):# I create the function merged_list
leftlist = ourlist[left:middle] # I define the leftlist
rightlist = ourlist[middle:right] # I define the right list
k = left # it is the the temporary variable
i = 0 # this variable that corespond to the index of the first group help me to iterate from left to right
j = 0 # this variable that corespond to the index of the second group help me to iterate from left to right
while (left + i < middle and middle+ j < right): # the condition that I want to achive before to stop my iteration
if (leftlist[i] <= rightlist[j]): #if the element in the leftlist is less or equal to the element in the rightlist
ourlist[k] = leftlist[i] # In this case I fill the value of the leftlist in ourlist with index k
i = i + 1 #now I have to increment the value by 1
else: # if the above codition is not match
ourlist[k] = rightlist[j] # I fill the rightlist element in ourlist with index k
j = j + 1 # I increment index j by 1
k = k+1 # now I increment the value of k by 1
if left + i < middle: # check if left + i is less than middle
ourlist[k] = leftlist[i] # I place all elements of my leftlist in ourlist
i = i + 1
k = k + 1
else: # otherwise if my leftlist is empty
while k < right: # untill k is less then right
ourlist[k] = rightlist[j] # I place all elements of rightlist in ourlist
j = j + 1
k = k + 1
ourlist = input('input - unordered elements: ').split() # insert the input and split
ourlist = [int(x) for x in ourlist]
merge_sort(ourlist, 0, len(ourlist))
print('output - ordered elements: ')
print(ourlist)
Out:
input - unordered elements: 15 1 19 93
output - ordered elements:
[1, 15, 19, 93]
*Bubble Sort → it first compares and then sorts adjacent elements if they are not in the specified order.
def bubble_sort(ourlist): # I create my function bubble_sort with the argument called ourlist
b=len(ourlist)-1 # for every list, I will have a minus 1 iteration
for x in range(b): # for each element in the range of b, I check if they are ordered or not
for y in range(b-x):
if ourlist[y]>ourlist[y+1]: # if one element is greater than the nearest elemnt in the list
ourlist[y],ourlist[y+1]=ourlist[y+1],ourlist[y] # I have to swap the elemnts, in other words
# I exchange the position of the two elements
return ourlist
ourlist=[15,1,9,3]
bubble_sort(ourlist)
Out:
[1, 3, 9, 15]
*Insertion Sort → it picks one item of a given list at the time and places it at the exact spot where it is to be placed.
def ins_sort(ourlist):
for x in range(1, len(ourlist)): # loop for each element starting from 1 to the length of our list
k = ourlist[x] # element with the index x
j = x-1 # j is the index previus the index x
while j >=0 and k < ourlist[j]: # untill each elermnt of the list are less than their previous element my loop don't stop
ourlist[j+1] = ourlist[j] # the elemnt indexed before the element considered is set to the next one index
j -= 1 # I decrement index j by 1
ourlist[j+1] = k # now k is the element in the index j+1
return ourlist
ourlist = [15, 1, 9, 3]
ins_sort(ourlist)
out:
[1, 3, 9, 15]
There are other Sorting Algorithms like Selection Sort and Shell Sort.
Searching Algorithms
*Searching algorithms are used to seek for some elements present in a given dataset. There are many types of search algorithms such as Linear Search, Binary Search, Exponential Search, Interpolation Search, and so on. In this section, we will see the Linear Search and Binary Search.
*Linear Search → in a single-dimensional array we have to search a particular key element. The input is the group of elements and the key element that we want to find. So, we have to compare the key element with each element of the group. In the following code, Lets try to seek element 27 in our list.
def lin_search(ourlist, key):
for index in range(0, len(ourlist)):
if (ourlist[index] == key):
return index
else:
return "not fund"
ourlist = [15, 1, 9, 3]
lin_search(ourlist, 27)
out:
'not fund'
*Binary Search → in this algorithm, we assume that the list is in ascending order. So, if the value of the search key is less than the element in the middle of the list, we narrow the interval to the lower half. Otherwise, we narrow to the upper half. We continue our check until the value is found or the list is empty.
def bin_search(ourlist, key):
left = 0 # I assign left position to zero
right = len(ourlist)-1 # I assign right position by defining the length of ourlist minus one
matched = False
while(left<=right and not matched): # the loop will continue untill the left element is less or equal to the right element and the matched is True
mid = (left+right)//2 # I find the position of the middle element
if ourlist[mid] == key: # if the middle element correponds to the key element
matched = True
else: #otherwise
if key < ourlist[mid]: # if key element is less than the middle element
right = mid - 1 #I assign the position of the right element as mid - 1
else: #otherwise
left = mid + 1 #left position will become the middle position plus 1
return matched
print(bin_search([1, 3, 9, 15], 17))
print(bin_search([1, 3, 9, 15], 3))
out:
False
True



Top comments (0)