My Final Project
OCLBHGS: OpenCL Barnes-Hut Galaxy Simulator (and its story)
In my 4th student year, I had a project with specific guidelines to follow. I was sure that I had a better method to solve the problem, a method that would tremendously improve the result beyond expectations, but it would cost me several points during the evaluation as some rules were broken ...
It taught me to trust my guts with more confidence.
Demo Link
No links to easily run the code as it is C + OpenCL. But all the code is available for you to check. I added this (heavy) GIF for a preview of the work. But I think the story behind it is way more interesting !
Link to Code
 mortimr
/
oclbhgs
mortimr
/
oclbhgs
🛰💫 OpenCL Barnes-Hut Galaxy Simulator | Fully exploiting the GPU to do massive data parallel computations in an n-body simulator
COMP426 Assignment 4
10K Body simulations examples, smooth 60FPS on GTX 1060
(Wait for gifs to properly load to see the simulations smoothly)
git checkout v1.0 to see this simulation
git checkout v1.1 to see this simulation
git checkout v1.2 to see this simulation
Running
Requires gcc, cmake, OpenCL, OpenGL and GLUT to run.
mkdir build
cd build
cmake
make
./oclbhgs
OpenCL Barnes-Hut Galaxy Simulator
| First Name | Last Name | Student ID |
|---|---|---|
| Iulian | Rotaru | 40102558 |
Introduction
The goal of this last assignement was to use OpenCL in order to compute an n-body simulation. The particularity with OpenCL is that kernels can be written for CPU or GPU devices To complete this project, I restarted the simulation from scratch in C99, I'll explain why in the report.
How was divided the work between the CPU and GPU in order to minimize data movements and synchronization ?
So, the…
How I built it (what's the stack? did I run into issues or discover something new along the way?)
This project was built in pure C95 and OpenCL. Why C95 ? Because OpenCL Kernels (code that is running in the devices like the CPU or the GPU to do parallel work) is C95, so it made things easier to have the host code (the one that prepares everything) and the code running in the devices (CPU / GPU) in the same language (no serialization, no classes, no conversions etc). I ran into a lot of issues, but everything is explained in the last section !
Additional Thoughts / Feelings / Stories
Right after my 3rd year at Epitech Paris, when my Bachelor cycle ended, I have been sent to Canada for 1 year of intense Software Engineering and CompSci courses at Concordia University. During this year, there was a project that really made me proud of myself. The class was Multicore Programming, and it was all about using all the available devices in our computers in order to perform parallel work. We had 4 projects during this class, and it was always the same problem, but with different tools. We had to make an n-body simulator able to run as much bodies as possible, and implementing the Barnes-Hut algorithm.
N-Body simulations
The main problem with n-body simulations is the fact that their computational complexity evolves exponentially. Bodies interact with each other in a specific manner: in our case, gravity had to be applied to the simulation. This means that the most basic approach for this problem is to take every single body and compute its speed & direction depending on the effects of gravity from EVERY other body of the simulation. Yes, this is by far the worst possible way of doing it, and this is why the n-body simulations can be "solved" by using different forms of parallelism. (By "solved", I mean enhanced, these problems have no perfect solutions that would work for any number of bodies).
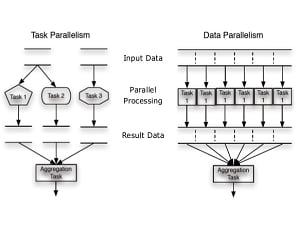
Types of parallelism
During our class, we learned about the two main types of parallelism: task parallelism and data parallelism. Task parallelism is when you run different types of actions & tasks in parallel. Data parallelism is when you run the exact same task, but on different data. Data parallelism is by far the best possible approach when trying to improve performances. Today's hardware (GPUs 👀) are built to execute simple tasks but on the largest data sets possible. It is absolutely great for things like image processing, but it could be applied to any sort of problem as long as the solution is properly shaped to run in a data parallel fashion.
Barnes-Hut algorithm
The Barnes-Hut algorithm is one of the solutions that exists to "solve" the n-body simulation. This is how it works:
- You create a quad-tree (a tree that has 4 children nodes for every node) that represents the space where the simulation is running. The first node is the complete width / height of the simulation. The 4 children nodes are the 4 quarters of their parent nodes.
- You place the bodies in this tree in order for the bodies to end up alone in one node (if multiple bodies exist in one node, we split the node into 4 and dispatch the bodies in the children, and we keep doing it until the bodies are alone)
- We define a threshold
Now when we want to compute the gravity pull between bodies, we are able to factorize it by computing it with a node of the tree and considering all the bodies contained in the children as one single body (mass center of all the bodies). And it is determined by running a formula (that you can find in the repository) and checking if the result is lower than the threshold: if it is, we factorize this node, otherwise we keep "digging" in the tree.
Putting it all together for the final challenge: OpenCL
Our last project was to port this algorithm to OpenCL, and run it both on the CPU and on the GPU. The evaluation gave us points for having both CPU and GPU kernels (code that you run on a device).
This is where I started to question this solution. What if I could only use the GPU for all the computation, and run massive data parallel tasks for all the steps of the algorithm ? Why would I need the CPU then ? One thing to know about the GPU is that it cannot access RAM memory like the CPU: yes, you have to copy from the CPU context (RAM) to the GPU context (one of the various memory regions from the device), and it is a massive overhead that could be completely deleted if the algorithm was refactored.
It finally hit me, the only problem came from the tree. A tree is a dynamic data structure. This means that there is a lot of allocation / de-allocation to do in order to make it work. And I was wondering: how can I keep using this algorithm, but have a static data structure to hold my bodies ?
As the number of bodies grew, everyone starts facing the same issue: when two bodies get extremely close to each other, they "dig" very very VERY deep in the tree, making the algorithm really slow. And this can be prevented by setting a maximal depth in our tree. This was a solution most of the students adopted, and it made me directly question the need for a dynamic data structure. The quad-tree is very interesting for the algorithm, but very bad for the GPU allocation.
The solution was simple => store the quad-tree inside a static 2D array. We knew the maximum size of this tree (because we now had a max depth), so we could compute the total number of nodes, pre-allocate everything and use a discriminant boolean value to know which nodes are active or not.
/--------|-------|
|0| |1|2|3|4| |5|6|7|8|9|10|11|12|13|...
\__|_______|
Then, from the position of the node, it became trivial to compute its spacial position, and also its depth in the tree. From this point, everything changed, and I started looking at the problem in a complete new way => how can I run everything on the GPU, and never rely on dynamic allocation or CPU kernels ?
And this is what I achieved in the end. While most implementations where allocating the tree in the RAM, and copying its state to the GPU when doing data parallel tasks, I actually allocated the tree ONCE when the program started, directly inside the GPU (and never again at runtime). And I only copied it out of the GPU for display purposes. All the steps from the algorithm have been revamped in order to work in a data parallel manner (working on the complete tree at once became trivial !). It was perfectly suited for the GPU. The performance boost was insane:
With Native Threads, I achieved smooth 700 body simulation.
With TBB, I also achieved smooth 700 body simulation.
With CUDA, task parallelism and data parallelism, I achieved smooth 1.5k simulation on GTX 1060.
With OpenCL, this "new" algorithm and only data parallelism, I achieved smooth 10k simulation on GTX 1060.
Here you can see some of the simulations I made (wait for the GIFs to properly load !)
10.000 bodies gravitating around 1 insanely heavy body

10.000 bodies with random masses and initial positions

In the end I didn't get all the points as I had no CPU kernels (😢), but who cares, I could handle a lot more bodies than the rest of the class 👍.
Hope you liked this little story :)










Top comments (7)
Whaaaa! This is sooooooo cooool! 🤯🤯🤯
Holy cow this is cool!!
Thanks Ben !✌️
I wonder if Barnes Hut algo is the best there is atm.
Wodnerful job its a task that I have been interested in seeing solved for one galaxy, so tens of billions of objects. How many RASPis and how much time would that take, what do you think?
about a million cores perhaps....
so in about 20 years or sooner we will be able to do it on a single GPU board
This is really cool.