Solve Leetcode Problems and Get Offers From Your Dream Companies||Minimum Path Sum

Leetcode Problem 64: Minimum Path Sum

In this series, I am going to solve Leetcode medium problems live with my friends, which you can see on our youtube channel. Today we will do Problem Leetcode: 64. Minimum Path Sum

A little bit about me, I have offers from Uber India and Amazon India in the past, and I am currently working for Booking.com in Amsterdam.

Motivation to learn algorithms

Solve Leetcode Problems and Get Offers From Your Dream Companies

Problem Statement

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time

Example 1:

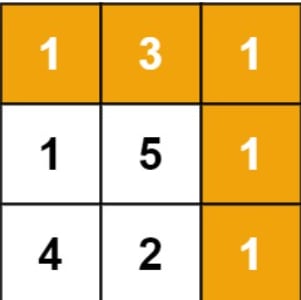
Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
Explanation: Because the path 1 → 3 → 1 → 1 → 1 minimizes the sum.

Example 2:

Input: grid = [[1,2,3],[4,5,6]]
Output: 12

Constraints:

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 200

• 0 <= grid[i][j] <= 100

Youtube Discussion

Solution

Approach 1: Brute Force

The Brute Force approach involves recursion. For each element, we consider two paths, rightwards and downwards, and find the minimum sum out of those two. It specifies whether we need to take the right step or a downward step to minimize the sum.

cost(i, j) = grid[i][j] + min(cost(i+1, j), cost(i, j+1))

The following code implements this algorithm:

C++ Solution

	class Solution {
	public:
	int minPathSum(vector<vector<int>>& grid)
	{
	return calculate(grid, 0, 0);
	}
	int calculate(vector<vector<int>>& grid, int i, int j)
	{
	if (i == grid.size() || j == grid[0].size())
	{
	return INT_MAX;
	}
	if (i == grid.size() - 1 && j == grid[0].size() - 1)
	{
	return grid[i][j];
	}
	return grid[i][j] +
	min(calculate(grid, i + 1, j), calculate(grid, i, j + 1));
	}
	};

view raw prob64.java hosted with ❤ by GitHub

Java Solution

	class Solution {
	public int calculate(int[][] grid, int i, int j)
	{
	if (i == grid.length || j == grid[0].length)
	{
	return Integer.MAX_VALUE;
	}
	if (i == grid.length - 1 && j == grid[0].length - 1)
	{
	return grid[i][j];
	}
	return grid[i][j] +
	Math.min(calculate(grid, i + 1, j), calculate(grid, i, j + 1));
	}
	public int minPathSum(int[][] grid) {
	return calculate(grid, 0, 0);
	}
	}

view raw min.java hosted with ❤ by GitHub

Complexity Analysis

The time complexity is O(2^(m+n))

The time complexity is O(m+n)

We can solve this problem in O(n*m) time complexity.

The idea is to calculate, for each index(i, j) find the min path from the top left to the index (i, j).

First Row and Column Cases

In the first row, we can move only right, and hence to reach any index in the first row the min path sum is the sum of all elements from the top left to that index.

For the first column, we can move only down, and hence to reach any index in the first row the min path sum is the sum of all elements from the top left to that index.

Any other Case

Now to reach index (i, j) we have two options

1. we reach from the index (i-1,j)

2. or we reach from the index (i, j-1)

We will choose the minimum of these two indexes. If we apply the same intuition for the rest of the grid we will find the min path sum from the top left to right bottom.

C++ Solution

	class Solution {
	public:
	int minPathSum(vector<vector<int>>& grid)
	{
	int n=grid.size();
	int m=grid[0].size();
	//initialize 1st column
	for(int j=1;j<m;j++)
	{
	grid[0][j]=grid[0][j-1]+grid[0][j];
	}
	//initialize 1st row
	for(int i=1;i<n;i++)
	{
	grid[i][0]=grid[i-1][0]+grid[i][0];
	}
	for(int i=1;i<n;i++)
	{
	for(int j=1;j<m;j++)
	{
	grid[i][j]+=min(grid[i-1][j],grid[i][j-1]);
	//find minimum of top and left block cost
	}
	}
	return grid[n-1][m-1];
	}
	};

view raw prob64optimized.cpp hosted with ❤ by GitHub

Java Solution

	class Solution {
	public int minPathSum(int [][]grid)
	{
	int n=grid.length;
	int m=grid[0].length;
	//initialize 1st column
	for(int j=1;j<m;j++)
	{
	grid[0][j]=grid[0][j-1]+grid[0][j];
	}
	//initialize 1st row
	for(int i=1;i<n;i++)
	{
	grid[i][0]=grid[i-1][0]+grid[i][0];
	}
	for(int i=1;i<n;i++)
	{
	for(int j=1;j<m;j++)
	{
	grid[i][j]+=Math.min(grid[i-1][j],grid[i][j-1]);
	//find minimum of top and left block cost
	}
	}
	return grid[n-1][m-1];
	}
	};

view raw minoptimized.java hosted with ❤ by GitHub

Complexity Analysis

The time complexity is O(n*m)

The space complexity is O(1)

Thank You for reading and Follow this publication for more LeetCode problems!😃

LeetCode Simplified